Hallar área bajo una función

| 1 |

Halla el área que delimita la gráfica de la función f(x)=x^2-4x+3 con el eje de abscisas entre las rectas x=0 y x=2

SOLUCIÓN

Nos están pidiendo el área bajo una curva en el intervalo [0,2], es decir, el área limitada por la curva, el eje de abcisas y las rectas verticales x=0 y x=2.

Si miramos la teoría, debemos resolver la ecuación f(x)=0 y ver si alguna de las soluciones está dentro del intervalo.

En nuestro caso la función es f(x)=x^2-4x+3 y el intervalo [0,2]

Resolvemos x^2-4x+3=0 y obtenemos como soluciones x=3 y x=1. La solución x=1 si está dentro del intervalo [0,2], por tanto debemos considerarla y dividir el intervalo [0,2] en dos: [0,1] y [1,2] , quedando así nuestra fórmula para calcular el área:

A = \left|\int_0^1 (x^2-4x+3) dx \right|+ \left|\int_1^2 (x^2-4x+3) dx \right|

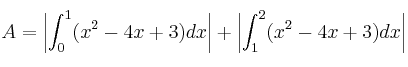
Calculamos primero la integral indefinida:

\int (x^2-4x+3) dx = \frac{x^3}{3} - \frac{4x^2}{2} + 3x = \frac{x^3}{3} - 2x^2 + 3x

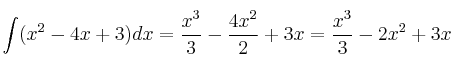
Y ahora le aplicamos los límites de integración

\int_0^1 (x^2-4x+3) dx= \left[ \frac{x^3}{3} - 2x^2 + 3x \right]_0^1 =

= \left[ \frac{1^3}{3} - 2 \cdot 1^2 + 3 \cdot 1 \right] - \left[ \frac{0^3}{3} - 2 \cdot 0^2 + 3 \cdot 0 \right] = \frac{4}{3}

\int_1^2 (x^2-4x+3) dx= \left[ \frac{x^3}{3} - 2x^2 + 3x \right]_1^2 =

= \left[ \frac{2^3}{3} - 2 \cdot 2^2 + 3 \cdot 2 \right] - \left[ \frac{1^3}{3} - 2 \cdot 1^2 + 3 \cdot 1 \right] = \frac{2}{3} -\frac{4}{3} = \frac{-2}{3}

Recordemos que tenemos que expresarlo en valor absoluto

A = \left|\int_0^1 (x^2-4x+3) dx \right|+ \left|\int_1^2 (x^2-4x+3) dx \right| = \left| \frac{4}{3} \right| + \left| \frac{-2}{3} \right| = \frac{6}{3} = 2 \: u^2

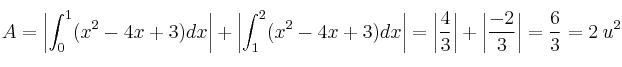
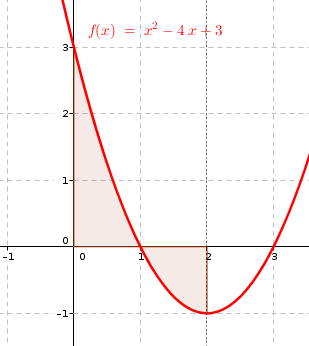
En la siguiente imagen podemos ver como el área representa 2 unidades cuadradas