Posición Relativa Recta-Circunferencia

, por dani

|

Para hallar la posición relativa entre recta y circunferencia podemos usar dos métodos:

Uno de ellos es resolviendo el sistema de ecuaciones:

\left. 2x+y-12=0 \atop x^2+y^2-4x+2y+2=0 \right\}

Vamos a resolver por sustitución. Despejamos «y» en la primera ecuación y sustituimos en la segunda ecuación

y=-2x+12

x^2+(-2x+12)^2-4x+2(-2x+12)+2=0
x^2+4x^2+144-48x-4x-4x+24+2=0
5x^2-56x+170=0

Resolvemos la ecuación de segundo grado:

\begin{array}{ccc} & & Sin \:\: solución\\ & \nearrow &\\ x=\frac{-(-56)\pm \sqrt{(-56)^2-4 \cdot5\cdot170}}{2 \cdot5}= \frac{56\pm \sqrt{-264}}{10}& &\\ & \searrow &\\& &Sin \:\: solución\end{array}

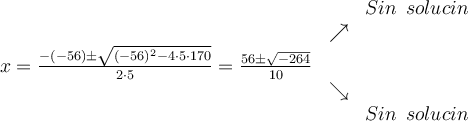
No haya solución, por tanto la recta y la circunferencia no tienen ningún punto en común: la recta es exterior a la circunferencia

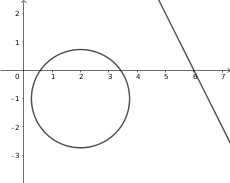
Recta exterior a circunferencia
Posición relativa de recta y circunferencia
matematicasies.com

Halla la posición relativa de la recta 2x+y-12=0 y la circunferencia x^2+y^2-4x+2y+2=0