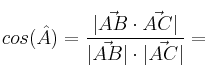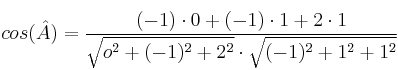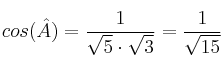Selectividad Andalucía 2019 Junio B4

|

Considera el triángulo cuyos vértices son los puntos A(1,1,0) , B(1,0,2) y C(0,2,1.

– a) Halla el área de dicho triángulo.
– b) Calcula el coseno del ángulo en el vértice A

SOLUCIÓN

Dados los puntos A(1,1,0) , B(1,0,2) y C(0,2,1, podemos formar los vectores:
\vec{AB}=(0,-1,2)
\vec{AC}=(-1,1,1)

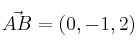
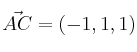
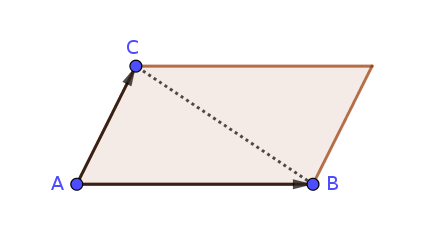
El producto vectorial nos da el área del paralelogramo.
La mitad es el área del triángulo

A_{\triangle} = \frac{1}{2} \cdot |\vec{AB} \times \vec{AC}|

\vec{AB} \times \vec{AC} = \left| \begin{array}{ccc} \vec{i} &\vec{j} &\vec{k} \\ 0 & -1 & 1 \\ -1 & 1 & 1 \end{array} \right| = -3\vec{i} -2\vec{j} -\vec{k}
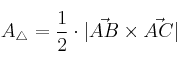
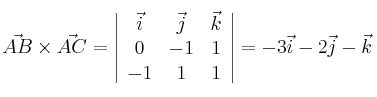
Por tanto 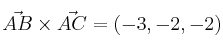\vec{AB} \times \vec{AC} =(-3,-2,-2)

A_{\triangle} = \frac{1}{2} \cdot \sqrt{(-3)^2+(-2)^2+(-1)^2}=\frac{1}{2}\sqrt{14} \:u^2


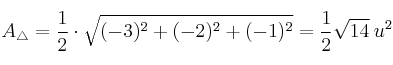
(El u^2 significa unidades cuadradas)

– b) De la fórmula del producto escalar: 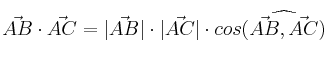\vec{AB} \cdot \vec{AC} = |\vec{AB}| \cdot |\vec{AC}| \cdot cos(\widehat{\vec{AB},\vec{AC}}),
despejaremos el coseno:
cos(\hat{A}) = \frac{|\vec{AB} \cdot \vec{AC}|}{|\vec{AB}| \cdot |\vec{AC}|}=
cos(\hat{A}) =\frac{(-1)\cdot 0 + (-1) \cdot 1 + 2 \cdot 1}{\sqrt{o^2+(-1)^2+2^2} \cdot \sqrt{(-1)^2+1^2+1^2}}

cos(\hat{A}) =\frac{1}{\sqrt{5}\cdot \sqrt{3}} = \frac{1}{\sqrt{15}}