Vector determinado por dos puntos
Dos puntos en el espacio 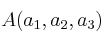 y
y 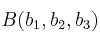
determinan un vector 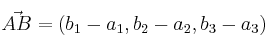
Módulo de un vector
Dado un vector 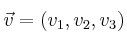 , podemos calcular su longitud o módulo con la fórmula:
, podemos calcular su longitud o módulo con la fórmula:
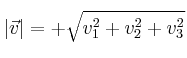
Suma y resta de vectores
Dados los vectores 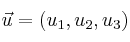 y
y 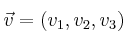 , podemos sumarlos o restarlos de la siguiente manera:
, podemos sumarlos o restarlos de la siguiente manera:
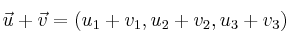
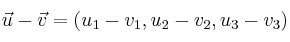
Producto por un número
Para multiplicar un vector por un número, multiplicamos cada una de las componentes del vector por dicho número
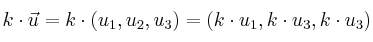
– Ejemplo: Dados los vectores 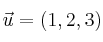 y
y 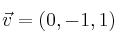 , calcula
, calcula 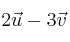
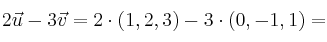
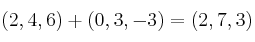
Otras operaciones con vectores:
– producto escalar
– producto vectorial
– producto mixto