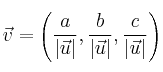– Dos vectores son paralelos cuando sean proporcionales
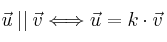
– Dos vectores son ortogonales (perpendiculares) cuando su producto escalar sea nulo
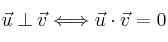
– Obtener un vector ortogonal a uno dado
Dado el vector 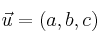 , se puede conseguir un vector ortogonal a
, se puede conseguir un vector ortogonal a 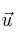 de la siguiente forma:
de la siguiente forma: 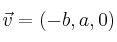
– Obtener un vector unitario y paralelo a uno dado.
Dado el vector 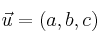 , podemos conseguir un vector paralelo a
, podemos conseguir un vector paralelo a 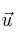 y además unitario (de módulo 1) de la siguiente forma:
y además unitario (de módulo 1) de la siguiente forma: