Una ecuación es una igualdad de expresiones algebraicas que sólo se cumple para determinados valores de las letras (o incógnitas).

Ejemplos de ecuaciones:

– 
– 

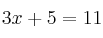
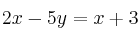
Partes de una ecuación

Como ejemplo tomamos la ecuación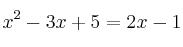

– Miembros: cada uno de los lados del signo igual.
Miembro de la izquierda: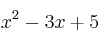
Miembro de la derecha:

– Términos: cada uno de los monomios de la ecuación. En el ejemplo los términos son: , , , ,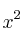

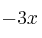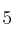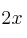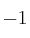
– Incógnitas: valores desconocidos que se representan con letras (x, y, ..). En el ejemplo hay una sola incógnita: 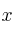(no importa que aparezca varias veces, o elevada a un exponente)

– Grado: mayor de los exponentes. En el ejemplo: grado 2

– Solución: las soluciones son números que al sustituirlos por las incógnitas, cumplen la igualdad. En el ejemplo, una solución es "3" porque si sustituimos la "x" por "3", se cumple la igualdad:

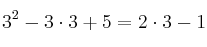
Tipos de ecuaciones

En una primera clasificación podemos distinguir varios tipos de ecuaciones:

– según el número de incógnitas
– según el grado

Ejemplos:

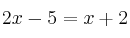–  (Ecuación de primer grado con una incógnita)
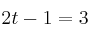–  (Ecuación de primer grado con una incógnita)
–  (Ecuación de segundo grado con una incógnita)
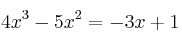–  (Ecuación de tercer grado con una incógnita)
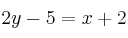–  (Ecuación de primer grado con dos incógnitas)