-
Un jugador profesional lanza un dado trucado. La probabilidad de cada una de las seis caras es:
, 
, 
, 
.
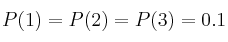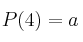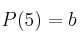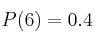Sabiendo que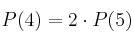 
:
– a) Calcula el valor de 
y 
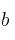
– b) ¿Qué cara debe pedir el jugador para ganar la partida?
-
Se tiene 2 urnas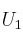 
y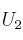 
cuyo contenido en bolas rojas, azules y verdes es:
en la urna 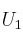4 bolas azules, 3 bolas rojas y 3 verdes, en la urna 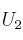4 rojas, 5 azules y 1 verde.
Se lanzan 3 monedas y se obtienen exactamente 2 caras seguidas se extrae una bola de la urna 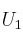, en otro caso se extrae de la urna 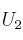. Se pide:
– a) Espacio muestral para el experimento aleatorio de lanzar 3 monedas.
– b) Calcular la probabilidad de que la bola extraída sea azul.
-
La probabilidad de un suceso 
es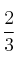 
, la de un suceso 
es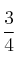 
y la de la intersección es 
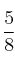. Calcula de forma razonada la probabilidad de que:
– a) Se verifique alguno de los sucesos
– b) No se verifique ni A ni B
– c) Ocurra A si se ha verificado B
-
En una determinada ciudad, aparte de su propia lengua, el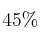 
de los habitantes hablan inglés, el 
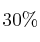francés, y el 
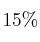inglés y francés. Calcula la probabilidad de que:
– a) Un habitante elegido al azar de entre los que hablan francés, hable también inglés.
– b) Un habitante de esta ciudad elegido al azar no hable ni inglés ni francés.
-
En un colegio hay 120 alumnos que cursan el bachillerato, 80 de ellos son de primero. Del total hay 64 chicas y 45 son chicas de primero. Elegimos un alumno al azar, se pide de forma razonada:
– a) ¿Cuál es la probabilidad de que el alumno elegido sea chico de segundo?.
– b) Si el alumno elegido se sabe que es de primero, ¿cuál es la probabilidad de que sea chica
