-
Un estudio estadístico determina que la noche del 31 de diciembre conduce el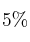 
de la población, el 
consume alcohol esa noche y el 
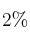conduce y consume alcohol.
– a) ¿Son independientes los sucesos “conducir” y “consumir alcohol”?
– b) ¿Qué porcentaje de la población no conduce ni consume alcohol esa
noche?
– c) De las personas que consumen alcohol, ¿qué porcentaje conduce esa
noche?
-
– a) Calcule la probabilidad de que al lanzar dos dados, la suma de sus puntuaciones sea un múltiplo de 4.
– b) De un experimento aleatorio se conocen las siguientes probabilidades
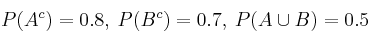
¿Son A y B incompatibles?
-
De los 700 alumnos matriculados en una asignatura, 210 son hombres y 490 mujeres. Se sabe que el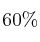 
de los hombres y el 
de las mujeres aprueban dicha asignatura. Se elige una persona al azar.
– a) ¿Cuál es la probabilidad de que apruebe la asignatura?
– b) Sabiendo que ha aprobado la asignatura, ¿cuál es la probabilidad de que
sea una mujer?
-
En una urna A hay 8 bolas verdes y 6 rojas. En otra urna B hay 4 bolas verdes, 5 rojas y 1 negra. Se lanza un dado, si sale un número menor que 3 se saca una bola de la urna A, y si sale mayor o igual que 3 se saca una bola de la urna B.
– a) Calcule la probabilidad de que la bola sea verde si ha salido un 4.
– b) Calcule la probabilidad de que la bola elegida sea roja.
– c) Sabiendo que ha salido una bola verde, ¿cuál es la probabilidad de que sea de la urna A?
-
Sean dos sucesos A y B tales que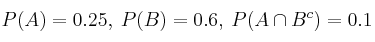 
.
– a) Calcule la probabilidad de que ocurra A y ocurra B.
– b) Calcule la probabilidad de que no ocurra A pero sí ocurra B.
– c) Calcule la probabilidad de que ocurra A sabiendo que ha ocurrido B.
– d) ¿Son independientes A y B?
Matemáticas IES
Matemat_Soc_Andalucia_2015
andalucía