Integrales. Área entre curvas

|

Calcula el área encerrada entre la parábola g(x)=-x^2+6x y las rectas h(x)=3x y i(x)=-3x+18

SOLUCIÓN

Veamos en qué puntos se cortan las funciones

g(x)=h(x) \longrightarrow -x^2+6x=3x
-x^2+3x=0 \longrightarrow \textcolor{blue}{x=0} y \textcolor{blue}{x=3}

g(x)=i(x) \longrightarrow -x^2+6x=-3x+18
-x^2+9x-18=0 \longrightarrow \textcolor{blue}{x=3} y \textcolor{blue}{x=6}

Dibujamos la recta h(x)=3x mediante dos puntos:

x=0 \longrightarrow y=3 \cdot 0 = 0 \longrightarrow \textcolor{red}{(0,0)}
x=3 \longrightarrow y=3 \cdot 3 = 9 \longrightarrow \textcolor{red}{(3,9)}

Dibujamos la recta i(x)=-3x+18 mediante dos puntos:

x=3 \longrightarrow y=-3 \cdot 3+18 = 9 \longrightarrow \textcolor{blue}{(3,9)}
x=6 \longrightarrow y=-3 \cdot 6+18 = 0 \longrightarrow \textcolor{blue}{(6,0)}

Dibujamos ahora la parábola.
Ya tenemos 3 puntos por los que pasa: \textcolor{green}{(0,0)} , \textcolor{green}{(6,0)} y \textcolor{green}{(3,9)}

Calculamos el vértice:
x=\frac{-b}{2a} \longrightarrow x=\frac{-5}{2 \cdot (-1)}=3
Por tanto el vértice es el punto \textcolor{green}{(3,9)}

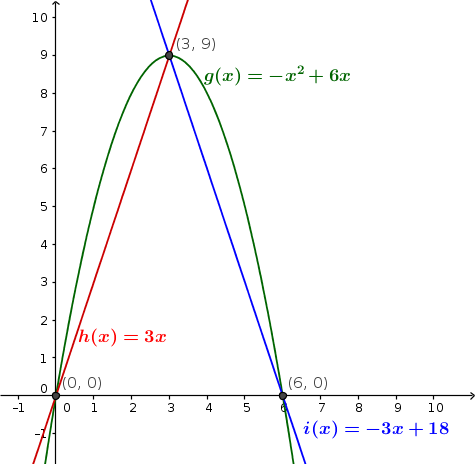
A partir de la gráfica calculamos el área:

A=\int_0^3 [-x^2+6x -(3x)]dx + \int_3^6 [-x^2+6x -(-3x+18)]dx=

\int_0^3 (-x^2+3x)dx + \int_3^6 (-x^2+9x -18)dx=

\left[ \frac{-x^3}{3}+\frac{3x^2}{2} \right]_0^3+\left[ \frac{-x^3}{3}+\frac{9x^2}{2}-18x \right]_3^6=

\left( \frac{-3^3}{3}+\frac{3\cdot 3^2}{2} \right) - \left( \frac{-0^3}{3}+\frac{3 \cdot 0^2}{2} \right) +

+\left( \frac{-6^3}{3}+\frac{9 \cdot 6^2}{2}-18 \cdot 6 \right) - \left( \frac{-3^3}{3}+\frac{9 \cdot 3^2}{2}-18 \cdot 3\right)=

4.5 - 0 -18 -(-22.5) = 4.5 + 4.5 = \fbox{9 u^2}