Ejercicios de Probabilidad - Matemáticas Aplicadas a las C. S. II
(55) ejercicios de Probabilidad
-
Se consideran dos sucesos
 y
y  de un experimento aleatorio, tales que:
de un experimento aleatorio, tales que:
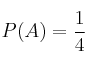 ,
, 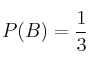 y
y 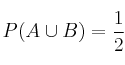
– a) ¿Son
 y
y  sucesos independientes? Razónese.
sucesos independientes? Razónese.
– b) Calcule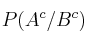
-
En un juego consistente en lanzar dos monedas indistinguibles y equilibradas y un dado de 6 caras equilibrado, un jugador gana si obtiene dos caras y un número par en el dado, o bien exactamente una cara y un número mayor o igual que cinco en el dado.
– a) Calcule la probabilidad de que un jugador gane
– b) Si se sabe que una persona ha ganado, ¿Cuál es la probabilidad de que obtuviera dos caras al lanzar las monedas? -
Sean
 y
y  dos sucesos tales que
dos sucesos tales que 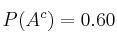 ,
, 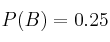 y
y 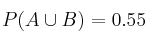
– (a) Razone si
 y
y  son independientes
son independientes
– (b) Calcule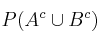
-
En cierto curso de un centro de enseñanza el 62,5 % de los alumnos aprobaron Matemáticas. por otro lado, entre quienes aprobaron Matemáticas el 80 % aprobó también Física. Se sabe igualmente que sólo el 33,3 % de quienes no aprobaron Matemáticas, aprobaron Física. Se pide razonadamente:
– a) ¿Qué porcentaje consiguió aprobar ambas asignaturas?
– b) ¿Cuál es el porcentaje de aprobados en la asignatura de Física?
– c) Si un estudiante no aprobó Física, ¿qué probabilidad hay de que aprobara Matemáticas? -
De los sucesos aleatorios
 y
y  del mismo espacio de sucesos se sabe que:
del mismo espacio de sucesos se sabe que:
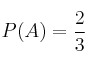 ,
, 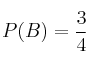 y
y 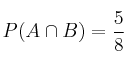 . Calcule:
. Calcule:– a) La probabilidad de que se verifique alguno de los dos sucesos.
– b) La probabilidad de que no ocurra ninguno de los dos sucesos.
– c) La probabilidad de que ocurra si se ha verificado
si se ha verificado  .
.
 Matemáticas IES
Matemáticas IES
