Ejercicios de Matemáticas Aplicadas a las Ciencias Sociales II (2º Bachillerato)

(37) ejercicios de Programación Lineal

(#610) Seleccionar

Un comerciante dispone de 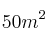$50 m^2$ de piel de armiño, 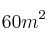$60 m^2$ de piel de zorro y 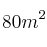$80 m^2$ de cuero. Fabrica dos tipos de abrigos: A y B. Para los abrigos de tipo A usa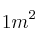 $1 m^2$
de piel de armiño,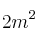 $2 m^2$ de piel de zorro y 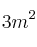$3 m^2$ de cuero. Para los abrigos de tipo B usa 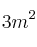$3 m^2$ de piel de armiño, 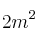$2 m^2$ de piel de zorro y 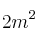$2 m^2$ de cuero. Los abrigos de tipo A los vende a 800€ y los de tipo B a 1900€. ¿cuántos abrigos tiene que fabricar de cada tipo para obtener unos ingresos máximos?
(#616) Seleccionar

Resuelve gráficamente el siguiente sistema de inecuaciones y calcula los vértices del recinto solución:

$\left. \begin{array}{lcr} 2x + y \leq 18 \\ 2x + 3y \leq 26 \\ x + y \leq 16 \\ x \geq 0 \\ y \geq 0 \end{array} \right\}$
(#655) Seleccionar

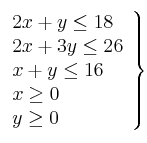
Un orfebre fabrica dos tipos de joyas. Las de tipo A precisan 1 gramo de oro y 1,5 gramos de plata, vendiéndolas a 40 euros cada una. Para la fabricación de las del tipo B emplea 1,5 gramos de oro y 1 gramo de plata y las vende a 50 euros. El orfebre tiene sólo en el taller 750 gramos de oro y 750 gramos de plata. ¿Cuántas joyas ha de fabricar de cada clase para obtener un ingreso máximo?
(#656) Seleccionar

Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada anterior. Para ello lanzan dos ofertas: A y B. La oferta A consiste en un lote de una camisa y un pantalón, que se vende a 30 euros. La oferta B consiste en un lote de 3 camisas y 1 pantalón y se vende a 50 euros. No se desea ofrecer menos de 20 lotes de la oferta A, ni menos de 10 lotes de la oferta B. ¿Cuántos lotes ha de vender de cada tipo para maximizar las ganancias?
(#3174) Seleccionar

Una imprenta local edita periódicos y revistas. Para cada periódico necesita un cartucho de tinta negra y otro de color, y para cada revista uno de tinta negra y dos de color. Si sólo dispone de 800 cartuchos de tinta negra y 1100 de color, y si no puede imprimir más de 400 revistas, ¿cuánto dinero podrá ingresar como máximo, si vende cada periódico a 0.9 euros y cada revista a 1.2 euros?