Ejercicios de Funciones y derivadas- Matemáticas Aplicadas a las C. S. II
(29) ejercicios de Funciones y Derivadas
-
Sean las funciones
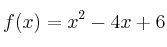 y
y 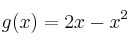
– (a) Determine, para cada una de ellas, los puntos de corte con los ejes, el vértice y la curvatura. Represéntelas gráficamente
– (b) Determine el valor de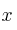 para el que se hace mínima la función
para el que se hace mínima la función 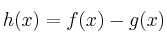 .
. -
Calcula las siguientes derivadas:
– (a)
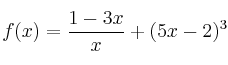
– (b)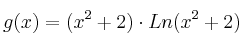
– (c)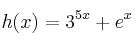
-
El beneficio obtenido por una empresa, en miles de euros, viene dado por la función
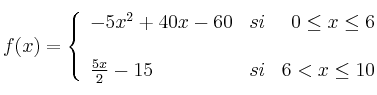
donde x representa el gasto en publicidad en miles de euros.
– a) Represente la función f .
– b) Calcule el gasto en publicidad a partir del cual la empresa no tiene pérdidas.
– c) ¿Para qué gastos en publicidad se producen beneficios nulos?
– d) Calcule el gasto en publicidad que produce máximo beneficio. ¿Cuál
es ese beneficio máximo? -
Tras un test realizado a un nuevo modelo de automóvil, se ha observado que el consumo de gasolina,
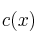 , expresado en litros, viene dado por la función
, expresado en litros, viene dado por la función
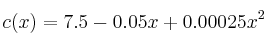
siendo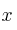 , la velocidad en
, la velocidad en 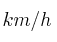
– a) Determine el consumo de gasolina a las velocidades de 50 km/h y 150 km/h.
– b) Estudie el crecimiento y decrecimiento de la función c(x) .
– c) ¿A qué velocidades de ese intervalo se obtiene el mínimo consumo y el máximo consumo y cuáles son éstos? -
Un banco lanza al mercado un plan de inversión cuya rentabilidad
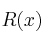 , en miles de euros, viene dada en función de la cantidad,
, en miles de euros, viene dada en función de la cantidad, 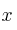 , que se invierte, también en miles de euros, por la siguiente expresión:
, que se invierte, también en miles de euros, por la siguiente expresión:
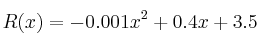 , con
, con 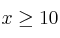 .
.– a) Calcule la rentabilidad para una inversión de 100000 euros.
– b) Deduzca y razone qué cantidad habría que invertir para obtener la máxima rentabilidad.
– c) ¿Qué rentabilidad máxima se obtendría?
 Matemáticas IES
Matemáticas IES
