Ejercicios de Matrices, Determinantes y Sistemas de Ecuaciones - 2º Bach. Sociales
(53) ejercicios de Matrices, Determinantes y Sistemas
-
Sea la matriz
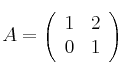
Hallar las matrices B que conmuten con A; es decir: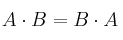
-
Calcula
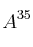 siendo A la siguiente matriz
siendo A la siguiente matriz
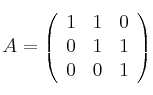
-
Calcula todos los productos posibles (de dos factores dsitintos) entre las siguientes matrices
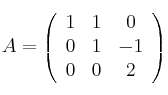

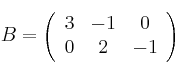
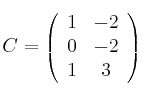

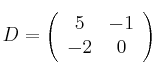
-
Dadas las matrices
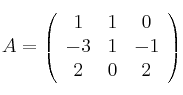

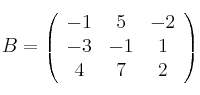
Se pide:
– a)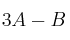
– b)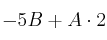
-
Calcula, si existe, la inversa de las siguientes matrices
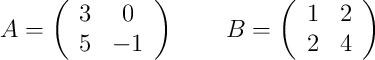
 Matemáticas IES
Matemáticas IES

