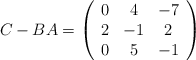Matrices: inversa y ecuación matricial

Dadas las matrices:

$A=\left( \begin{array}{ccc} 1&-2&3 \end{array}\right) \qquad B=\left( \begin{array}{c} 2\\-1\\1 \end{array}\right) \qquad C=\left( \begin{array}{ccc} 2&0&-1\\1&1&-1\\1&3&2 \end{array}\right)$

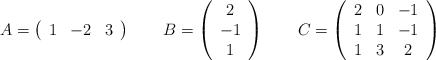
– a) Justifica si la matriz C tiene inversa
– b) Halla la inversa de C
– c) Resuelve la ecuación matricial

SOLUCIÓN

– a) Para que una matriz tenga inversa, su determinante tiene que ser distinto de cero.

$|C| = \left| \begin{array}{ccc} 2&0&-1\\1&1&-1\\1&3&2 \end{array}\right|=4-3+0+1+6-0=8 \neq 0 \longrightarrow \exists C^{-1}$
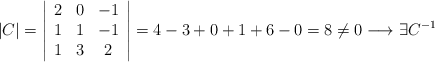
Por lo tanto C tiene inversa.

– b) Calculamos la inversa usando la fórmula:

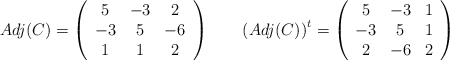
$C^{-1}=\frac{1}{|C|} \cdot \left( Adj(C)\right)^t$

$\alpha_{11}=\left|\begin{array}{cc}1&-1\\3&2\end{array}\right|=5 \qquad \alpha_{12}=\left|\begin{array}{cc}1&-1\\1&2\end{array}\right|=3 \qquad \alpha_{13}=\left|\begin{array}{cc}1&1\\1&3\end{array}\right|=2$

$\alpha_{21}=\left|\begin{array}{cc}0&-1\\3&2\end{array}\right|=3 \qquad \alpha_{22}=\left|\begin{array}{cc}2&-1\\1&2\end{array}\right|=5 \qquad \alpha_{23}=\left|\begin{array}{cc}2&0\\1&3\end{array}\right|=2$

$\alpha_{31}=\left|\begin{array}{cc}0&-1\\1&-1\end{array}\right|=1 \qquad \alpha_{32}=\left|\begin{array}{cc}2&-1\\1&-1\end{array}\right|=-1 \qquad \alpha_{33}=\left|\begin{array}{cc}2&0\\1&1\end{array}\right|=2$

$Adj(C)=\left(\begin{array}{ccc}5&-3&2\\-3&5&-6\\1&1&2 \end{array}\right) \qquad \left(Adj(C)\right)^t=\left(\begin{array}{ccc}5&-3&1\\-3&5&1\\2&-6&2 \end{array}\right)$

$C^{-1}=\frac{1}{|C|} \cdot \left( Adj(C)\right)^t=\frac{1}{8} \cdot \left(\begin{array}{ccc}5&-3&1\\-3&5&1\\2&-6&2 \end{array}\right) =\left(\begin{array}{ccc}\frac{5}{8}&\frac{-3}{8}&\frac{1}{8}\\\frac{-3}{8}&\frac{5}{8}&\frac{1}{8}\\\frac{1}{4}&\frac{-3}{4}&\frac{1}{4} \end{array}\right)$