🚀 Navega sin publicidad Regístrate GRATIS

Selectividad Andalucía 2012-2-B3

|

Se sabe que el 90% de los estudiantes del último curso de una Universidad está preocupado por sus posibilidades de encontrar trabajo, el 30% está preocupado por sus notas y el 25% por ambas cosas.

– a) Si hay 400 alumnos matriculados en el último curso de dicha Universidad, ¿cuántos de ellos no están preocupados por ninguna de las dos cosas?
– b) Si un alumno del último curso, elegido al azar, no está preocupado por encontrar trabajo, ¿cuál es la probabilidad de que esté preocupado por sus notas?

SOLUCIÓN

T = «Estar preocupado pro el Trabajo»
N = «Estar preocupado pro las Notas»

P(T)=0.90
P(N)=0.30
P(T \cap N)=0.25

– a) Nos piden P(T^c \cap N^c). Primero lo calculamos en probabilidad y después calculamos el número de alumnos. Aplicamos las leyes de Morgan:
P(T^c \cap N^c) = P(T \cup N)^c = 1 - P(T \cup N)
Necesitamos calcular la Probabilidad de la unión:
P(T \cup N) = P(T) + P(N) - P(T \cap N)=0.90+0.30-0.25=0.95
Por tanto:
P(T^c \cap N^c) = P(T \cup N)^c = 1 - P(T \cup N) = 1-0.95=0.05
Se lo aplicamos a los 400 alumnos y obtenemos:
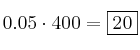0.05 \cdot 400 = \fbox{20} alumnos.

– b) P(N/T^c)=\frac{P(N \cap T^c)}{P(T^c)}=\frac{P(N)-P(N \cap T)}{P(T^c)}=\frac{0.30-0.25}{0.10}=\fbox{0.5}