Selectividad Andalucía 2012-6-A4
Un índice para calibrar la madurez lectora de los alumnos de primaria se distribuye
según una ley Normal con desviación típica 2. Elegida una muestra de 18 alumnos en un centro de primaria, se obtiene una media muestral de 10.8 en dicho índice. Mediante el uso de un contraste de hipótesis, ¿se puede aceptar, con un nivel de significación del 1%, la hipótesis nula de que la media del índice de madurez lectora de los alumnos de este centro no es inferior a 11?
SOLUCIÓN
Contraste
![]() (hipótesis nula: la media es mayor o igual a 11)
(hipótesis nula: la media es mayor o igual a 11)
![]() (hipótesis alternativa: la media es menor que 11)
(hipótesis alternativa: la media es menor que 11)
Región de aceptación (R)
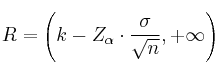
– ![]() : tamaño de la muestra
: tamaño de la muestra
– ![]() : desviación típica
: desviación típica
– ![]() : media de la muestra
: media de la muestra
– ![]() al
al ![]()
![]()
Miramos la tabla de la N(0,1) y vemos que el mas próximo a 0.99 es 0.9901.
Por tanto 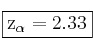
La región de aceptación quedaría:
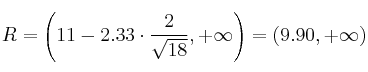
Toma de decisión
– Si ![]() aceptamos
aceptamos ![]()
– Si ![]() rechazamos
rechazamos ![]()
Como ![]() aceptamos
aceptamos ![]() y afirmamos que la media del índice de madurez lectora de los alumnos de este centro no es inferior a 11.
y afirmamos que la media del índice de madurez lectora de los alumnos de este centro no es inferior a 11.