-
(#4332) - Selectividad Andalucía 2019 Junio A1

Considera la función f definida por
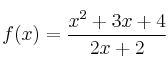 para
para 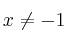
– a) Estudia y halla las asíntotas de la gráfica de f.
– b) Determina los intervalos de crecimiento y decrecimiento de f. -
(#4061) - Selectividad Andalucía 2014 - 1 - B2

Sea
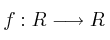 la función definida por
la función definida por 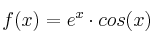
– a) Calcula la ecuación de la recta tangente a la gráfica de
 en el punto de abcisa
en el punto de abcisa 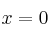
– b) Calcula la primitiva de cuya gráfica pasa por el punto
cuya gráfica pasa por el punto 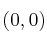
-
(#3723) - Selectividad Andalucía 2013 - J - B2

Sea
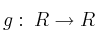 definida por
definida por 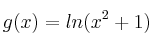 . Calcula la primitiva de
. Calcula la primitiva de 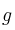 cuya gráfica pasa por el origen de coordenadas.
cuya gráfica pasa por el origen de coordenadas.
-
(#3721) - Selectividad Andalucía 2013 - J - B1

Sea
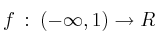 la función definida por
la función definida por
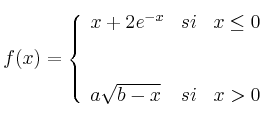
– a) Determina y
y 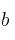 sabiendo que
sabiendo que  es derivable en todo su dominio.
es derivable en todo su dominio.
– b) Halla la ecuación de la recta tangente y de la recta normal a la gráfica en el punto de abcisa
en el punto de abcisa 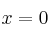
-
(#3641) - Selectividad Andalucía 2012 - 2 - B1

Sea la función
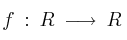 definida por
definida por 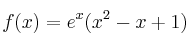
– a) Calcula
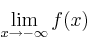 y
y 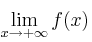
– b) Halla los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan), determinando si son máximos o mínimos.
– c) Determina las abscisas de los puntos de inflexión de la gráfica de .
.
(245) ejercicios de Matemáticas PAU Andalucía
(39) ejercicios de Matemáticas II - Análisis (Funciones, Continuidad, Límites, Derivadas e Integrales)
 Matemáticas IES
Matemáticas IES