-
(#3958) - Selectividad Andalucía 2019 Junio B3

Dadas las matrices
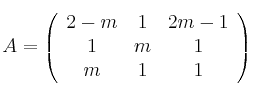 ,
, 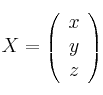 ,
, 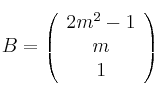 , considera el sistema de ecuaciones lineales dado por
, considera el sistema de ecuaciones lineales dado por 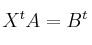 , donde
, donde 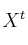 ,
, 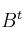 denotan las traspuestas. Discútelo según los distintos valores de m
denotan las traspuestas. Discútelo según los distintos valores de m -
(#3955) - Selectividad Andalucía 2019 Junio A3

Calcula todas las matrices
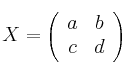 tales que
tales que 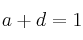 , tienen determinante 1 y cumplen
, tienen determinante 1 y cumplen 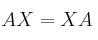 , siendo
, siendo 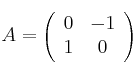
-
(#4391) - Selectividad Andalucía 2018 Septiembre B3

Considera el siguiente sistema de ecuaciones lineales
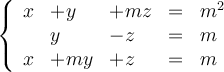
– a) Discute el sistema según los valores del parámetro

– b) Resuélvelo para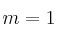 . Para dicho valor de
. Para dicho valor de  , calcula, si es posible, una solución en la que
, calcula, si es posible, una solución en la que 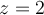
-
(#4390) - Selectividad Andalucía 2018 Septiembre A3

Considera las siguientes matrices
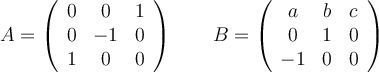
– a) Determina, si existen, los valores de a, b y c para los que las matrices A y B conmutan
– b) Calcula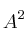 ,
, 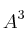 ,
, 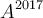 y
y 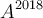
– c) Calcula, si existe, la matriz inversa de
-
(#3915) - Selectividad Andalucía 2013-2-A3

Considera las matrices
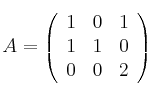 y
y
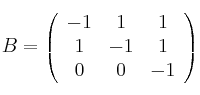
– (a) Halla, si es posible,
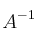 y
y 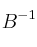
– (b) Halla el determinante de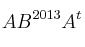 siendo
siendo 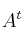 la matriz traspuesta de
la matriz traspuesta de 
– (c) Calcula la matriz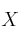 que satisface
que satisface 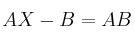
(245) ejercicios de Matemáticas PAU Andalucía
(66) ejercicios de Matemáticas II - Álgebra (Matrices, Determinantes y Sistemas)
 Matemáticas IES
Matemáticas IES