-
(#3052) - Selectividad Andalucía 2003-5-A1a

Sea la función
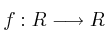 definida por:
definida por:
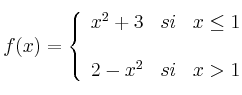
– (a) Calcula, si es posible, las derivadas laterales de
 en
en 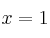
– (b) Halla los intervalos de crecimiento y de decrecimiento de la función
-
(#3049) - Selectividad Andalucía 2003-4-B2

Considera la función
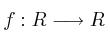 definida por
definida por 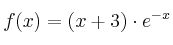
– (a) Halla las asíntotas de la gráfica de f
– (b) Determina los extremos relativos de f y los puntos de inflexión de su gráfica
– (c) Esboza la gráfica de f -
(#3048) - Selectividad Andalucía 2003-4-B1

Dadas la parábola de ecuación
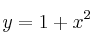 y la recta de ecuación
y la recta de ecuación 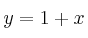 , se pide:
, se pide:– (a) Área de la región limitada por la recta y la parábola.
– (b) Ecuación de la recta paralela a la dada que es tangente a la parábola. -
(#3047) - Selectividad Andalucía 2003-4-A2

Se sabe que la función
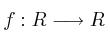 definida por
definida por 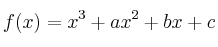
tiene un extremo relativo en el punto de abscisa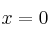 y que su gráfica tiene un punto de inflexión en el punto de abscisa
y que su gráfica tiene un punto de inflexión en el punto de abscisa 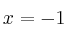 . Conociendo además que
. Conociendo además que 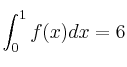 , halla
, halla  ,
, 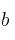 y
y 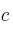 .
.
-
(#3046) - Selectividad Andalucía 2003-4-A1

Sea
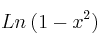 el logaritmo neperiano de
el logaritmo neperiano de 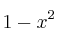 y sea
y sea 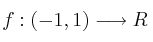 la
la
función definida por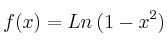 . Calcula la primitiva de f cuya gráfica pasa por el punto
. Calcula la primitiva de f cuya gráfica pasa por el punto 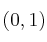 .
.
(245) ejercicios de Matemáticas PAU Andalucía
(39) ejercicios de Matemáticas II - Análisis (Funciones, Continuidad, Límites, Derivadas e Integrales)
 Matemáticas IES
Matemáticas IES