-
(#2697) - Selectividad Andalucía Septiembre 2018 B2

El beneficio, en miles de euros, que ha obtenido una almazara a lo largo de 50 años de vida viene dado por la expresión
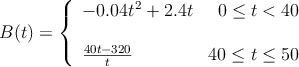
donde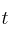 es el tiempo transcurrido.
es el tiempo transcurrido.– a) Estudie la continuidad y la derivabilidad de la función
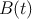 en el intervalo
en el intervalo ![[0,50] [0,50]](local/cache-TeX/99551ec2a731e6cc48cbec9785021fd1.png) .
.
– b) Estudie la monotonía de la función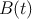 y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
– c) Represente la gráfica de la función y explique la evolución del beneficio. -
(#4398) - Selectividad Andalucía 2018 Septiembre suplente B2

– a) Calcule la derivada de las funciones

– b) Obtenga la ecuación de la recta tangente a la gráfica de la función
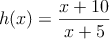 , el punto de abscisa
, el punto de abscisa 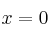
-
(#4397) - Selectividad Andalucía 2018 Septiembre suplente A2

Se considera la función
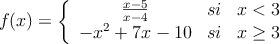
– a) Estudie la continuidad y la derivabilidad de la función

– b) Calcule los puntos de corte de la gráfica de con los ejes de coordenadas.
con los ejes de coordenadas.
– c) Calcule las asíntotas de , en caso de que existan.
, en caso de que existan. -
(#2745) - Selectividad Andalucía 2018 Septiembre A2

El consumo de cereales en una ciudad, en miles de toneladas, viene dado por la función
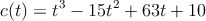 , para
, para 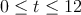 , donde
, donde 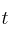 representa el tiempo.
representa el tiempo.– a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
– b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
– c) Represente gráficamente la función. -
(#3938) - Selectividad Andalucía 2013-2-A2

En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días trabajados según la función
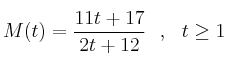 ,
,
donde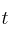 es el número de días trabajados.
es el número de días trabajados.– a) ¿Cuántos montajes realiza el primer día? ¿Cuántos días necesitará para
realizar cinco montajes diarios?
– b) ¿Qué ocurriría con el número de montajes diarios si trabajara indefinidamente?
– c) El dueño de la empresa cree que el número de montajes diarios aumenta con los días de trabajo. Estudiando la función, justifique si es cierta dicha creencia.
– d) Dibuje la gráfica de la función.
(245) ejercicios de Matemáticas PAU Andalucía
(22) ejercicios de Mat. C. Sociales II - Análisis (Funciones, Continuidad, Límites y Derivadas)
 Matemáticas IES
Matemáticas IES