-
El gerente de una empresa sabe que los beneficios de la misma,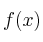 
, dependen de la inversión, 
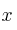, según la función 
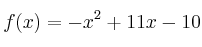. (x es la cantidad invertida en millones de euros).
– a) Determine los valores de la inversión para los que la función beneficio es no negativa.
– b) Halle el valor de la inversión para el cual el beneficio es máximo. ¿A cuánto asciende éste?
– c) ¿Entre qué valores ha de estar comprendida la inversión para que el beneficio sea creciente, sabiendo que éste es no negativo?
-
Sea la función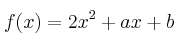 
– a) Determine los valores de 
y 
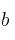sabiendo que su gráfica pasa por el punto 
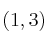y alcanza un extremo local en el punto de abscisa 
.
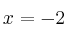– b) Tomando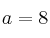 
y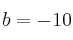 
deduzca la curvatura de su gráfica, el valor mínimo que alcanza la función y los valores donde la función se anula.
-
En los individuos de una población, la concentración de una proteína en sangre se distribuye según una ley Normal de media desconocida y desviación típica 0.42 g/dl. Se toma una muestra aleatoria de 49 individuos y se obtiene una media muestral de 6.85 g/dl.
– a) Obtenga un intervalo de confianza, al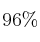 
, para estimar la concentración media de la proteína en sangre de los individuos de esa población.
– b) ¿Es suficiente el tamaño de esa muestra para obtener un intervalo de confianza, al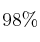 
, con un error menor que 0.125 g/dl?
-
En el experimento aleatorio consistente en lanzar un dado equilibrado con las caras numeradas del 1 al 6 y observar el resultado se consideran los siguientes sucesos: A: “obtener un número mayor que 4”, B: “obtener un número par”.
a) Escriba los elementos de cada uno de los siguientes sucesos:
; 
; 
; 
; 
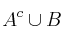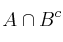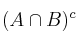
b) Calcule las probabilidades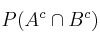 
y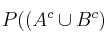 
-
a) Dibuje el recinto del plano definido por las inecuaciones:
; 
; 
; 
; 
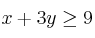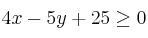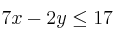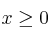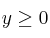
b) Calcule los vértices del mismo
c) Obtenga en dicho recinto los valores máximo y mínimo de la función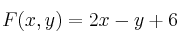 
y los puntos donde se alcanzan.
Matemáticas IES
Matemat_Soc_Andalucia_2010
andalucía