Ejercicios de Análisis matemático: Funciones, Límites, Derivadas e Integrales

(132) ejercicios de Funciones, Derivadas e Integrales

(#4028) Seleccionar

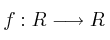Sea $f : R \longrightarrow R$ la función definida por 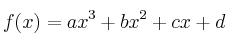$f(x)=ax^3+bx^2+cx+d$ . Calcula los valores de a, b, c y d sabiendo que f verifica:

– El punto (0,1) es un punto de inflexión de la gráfica de f
– f tiene un mínimo local en el punto de abcisa x=1
– La recta tangente a la gráfica de f en el punto de abcisa x=2 tiene pendiente 1
(#4029) Seleccionar

Se divide un segmento de longitud L=20 cm. en dos trozos. Con uno de los trozos se forma un cuadrado y con el otro un rectángulo en el que la base es el doble que la altura. Calcula la longitud de cada uno de los trozos para que la suma de las áreas del cuadrado y del rectángulo sea mínima
(#4030) Seleccionar

De entre todos los rectángulos cuya área mide 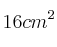$16 cm^2$ , determina las dimensiones del que tiene diagonal de menor longitud
(#4031) Seleccionar

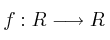Sea $f : R \longrightarrow R$ la función definida por

$f(x)= \left\{ \begin{array}{lcc} \frac{1}{x-1} & si & x < 0 \\ \\ x^2-3x-1 & si & x \geq 0 \end{array} \right.$

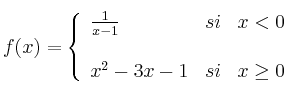
– a) Estudia la continuidad y dervabilidad
– b) Determina sus asíntotas y sus extremos relativos
– c) Esboza la gráfica de f
(#4032) Seleccionar

Se sabe que la función $f: R \longrightarrow R$ definida por

$f(x) = ax^3+bx^2+cx+d$

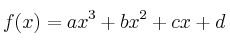
tiene extremos relativos en (0,0) y en (2,2). Calcula a,b,c,d