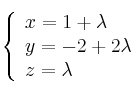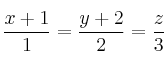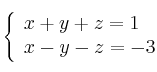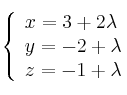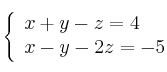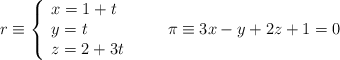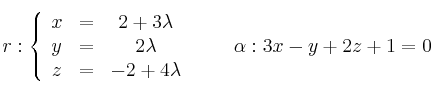EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
Dados los siguientes vectores
![]()
Se pide:
a) Efectúa la operación ![]()
b) Comprueba si los tres vectores forman una base de ![]()
Considere las siguientes rectas:
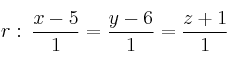 y
y
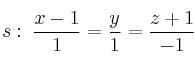
a) Estudie la posición relativa de ambas rectas.
b) En caso de que las rectas se corten, calcule el plano que las contiene y el ángulo que forman ambas rectas. En caso de que las rectas se crucen, calcule la perpendicular común a ambas rectas.
Resuelve los siguientes apartados:
– a) Calcular la ecuación del plano ![]() que pasa por
que pasa por ![]() y es perpendicular a la recta
y es perpendicular a la recta
![]()
– b) Corta el plano anterior con los tres ejes de coordenadas y obtendrás tres puntos A, B y C. Calcula el Volumen del tetraedro que determinan.
Halla la ecuación del plano que contiene a la recta ![]() de ecuaciones
de ecuaciones
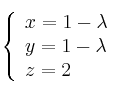
y es paralelo a la recta ![]() definida por
definida por
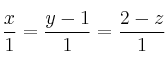
Calcular la ecuación del plano que pasa por ![]() y
y ![]() y es paralelo a la recta
y es paralelo a la recta ![]()
Estudiar la posición relativa de los siguientes planos según los posibles valores del parámetro ![]() , siendo:
, siendo:
![]()
![]()
![]()
 Matemáticas IES
Matemáticas IES