-
(#3271) - Selectividad Andalucía 2007-1-B1

Un Ayuntamiento concede licencia para la construcción de una urbanización de a lo sumo 120 viviendas, de dos tipos A y B.
Para ello la empresa constructora dispone de un capital máximo de 15 millones de euros, siendo el coste de construcción de la vivienda de tipo A de 100000 euros y la de tipo B 300000 euros.
Si el beneficio obtenido por la venta de una vivienda de tipo A asciende a 20000 euros y por una de tipo B a 40000 euros, ¿cuántas viviendas de cada tipo deben construirse para obtener un beneficio máximo? -
(#3174) - Selectividad Andalucía 2006-1-A1

Una imprenta local edita periódicos y revistas. Para cada periódico necesita un cartucho de tinta negra y otro de color, y para cada revista uno de tinta negra y dos de color. Si sólo dispone de 800 cartuchos de tinta negra y 1100 de color, y si no puede imprimir más de 400 revistas, ¿cuánto dinero podrá ingresar como máximo, si vende cada periódico a 0.9 euros y cada revista a 1.2 euros?
-
(#4165) - Selectividad Andalucía 2001-6-B1

Sea el recinto definido por las siguientes inecuaciones:
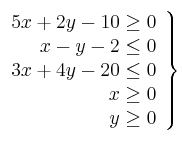
– a) Dibuje dicho recinto y determine sus vértices.
– b) Determine en qué punto de ese recinto alcanza la función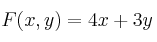 el máximo valor.
el máximo valor. -
(#4164) - Selectividad Andalucía 2001-2-A1

Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar 1600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A cuesta 4 millones de pts y puede transportar 200 personas y 6 toneladas de equipaje; la contratación de uno del tipo B cuesta 1 millón de pts y puede transportar 100 personas y 15 toneladas de equipaje.
¿Cuántos aviones de cada tipo deben utilizarse para que el coste sea mínimo?.
(245) ejercicios de Matemáticas PAU Andalucía
(19) ejercicios de Mat. C. Sociales II - Programación Lineal (Optimización, Sistemas de Inecuaciones)
 Matemáticas IES
Matemáticas IES