Ejercicios de Ejercicios de Geometría en el espacio. Bachillerato
(103) ejercicios de Geometría en el Espacio
-
Estudia las posiciones relativas de la recta
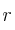 y el plano
y el plano 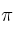 de ecuaciones:
de ecuaciones: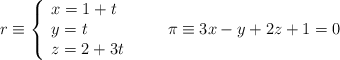
-
Calcula el ángulo que forman las rectas
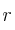 y
y 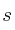 , siendo sus ecuaciones las siguientes:
, siendo sus ecuaciones las siguientes: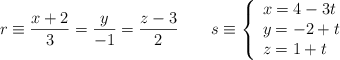
-
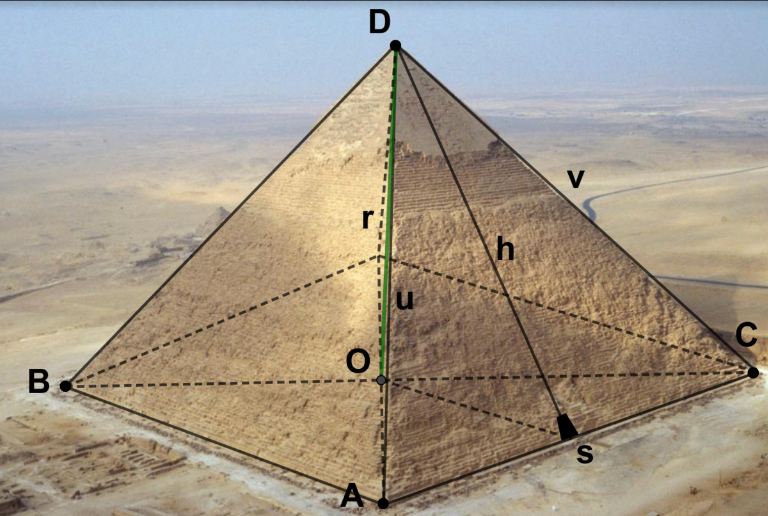
La Gran Pirámide de Guiza (también conocida como Pirámide de Keops o de Jufu) es la más antigua de las siete maravillas del mundo y la única que aún perdura, además de ser la mayor de las pirámides de Egipto. Ayúdanos a conocer un poco más de la Gran Pirámide, siguiendo los siguientes pasos:
 Ejercicio: Plano que pasa por 3 puntos
Ejercicio: Plano que pasa por 3 puntos1) La base de la pirámide está formada por los cuatro puntos de los cuales tres puntos son
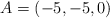 ,
, 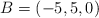 y
y 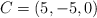 . Forma los vectores
. Forma los vectores 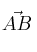 y
y 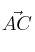 , comprueba que son linealmente independientes y calcula el área del paralelogramo que forman haciendo uso del producto vectorial. Sabiendo que la longitud es
, comprueba que son linealmente independientes y calcula el área del paralelogramo que forman haciendo uso del producto vectorial. Sabiendo que la longitud es 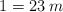 y por tanto la superficie es
y por tanto la superficie es 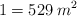 ¿Cuántos metros cuadrados de superficie tiene la Gran Pirámide?
¿Cuántos metros cuadrados de superficie tiene la Gran Pirámide?2) Si la vertical del centro de la pirámide sigue esta ecuación:
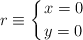
Y el lado de la puerta (donde está el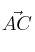 ) es la recta de ecuación:
) es la recta de ecuación:
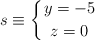
¿Cuántos metros hay de la puerta al centro de la pirámide, O? Demuéstralo con la distancia entre dos rectas (1=23 m)
3) Sabiendo que la cúspide (D) está en el
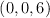 calcular las ecuaciones vectoriales y paramétricas de las dos rectas
calcular las ecuaciones vectoriales y paramétricas de las dos rectas 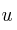 y
y 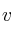 que forma los lados (
que forma los lados (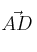 y
y 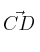 )
)4) Halla el plano que contiene a la puerta
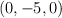 y es un lado de la pirámide. Halla el plano que es vertical y contiene a la puerta y al centro O. Interseca ambos planos obteniendo la ecuación de la recta
y es un lado de la pirámide. Halla el plano que es vertical y contiene a la puerta y al centro O. Interseca ambos planos obteniendo la ecuación de la recta 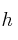 . Comprueba que es la misma recta que pasa por la puerta y la cúspide D.
. Comprueba que es la misma recta que pasa por la puerta y la cúspide D.
 Matemáticas IES
Matemáticas IES
