Ejercicios de Ejercicios de Geometría en el espacio. Bachillerato

(103) ejercicios de Geometría en el Espacio

(#4482) Seleccionar

Estudiar la posición relativa de los siguientes planos según los posibles valores del parámetro $a$ , siendo:
$\pi_1= 4x+2y+2z=2a$
$\pi_2= ax+y+z=1$
$\pi_3= 2x+y+az=1$
(#4531) Seleccionar

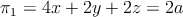
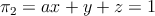
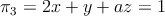
Demuestre que los tres puntos (1,-1, 3), (2, 1 ,7) y (4, 2, 6) son los vértices de un triángulo rectángulo y calcule su área.
(#4566) Seleccionar

Dados los vectores 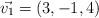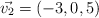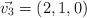$\vec{v_1}=(3,-1,4)$ ; $\vec{v_2}=(-3,0,5)$ ; $\vec{v_3}=(2,1,0)$ se pide:

a) ¿Forman una base de 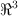${\Re}^3$ ? ¿Por qué?

b) Realiza las siguientes operaciones:
- b1) $\vec{v_1} - (\vec{v_2} - 2 \vec{v_3})$
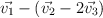
- b2) $\vec{v_2} \cdot \vec{v_3}$
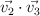
- b3) $\vec{v_1} \times \vec{v_3}$
(#4567) Seleccionar

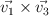
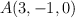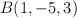Dados los puntos $A(3, -1, 0)$ y $B(1, -5, 3)$ se considera la recta 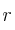$r$ que pasa por ambos. Se pide:

a) Halla un vector director de 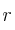$r$ .

b) Obtén la ecuación vectorial, paramétrica, continua e implícita (o general) de 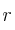$r$ .
(#4568) Seleccionar

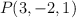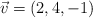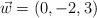Dados el punto $P(3, -2, 1)$ y los vectores $\vec{v}=(2,4,-1)$ y $\vec{w}=(0,-2,3)$ se pide:

a) Halla la ecuación vectorial, paramétrica e implícita (o general) del plano 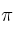$\pi$ que forman.

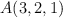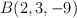b) Comprueba si los puntos $A(3, 2, 1)$ y $B(2, 3, -9)$ pertenecen o no al plano $\pi$ .