Ejercicios de Ejercicios de Geometría en el espacio. Bachillerato

(103) ejercicios de Geometría en el Espacio

(#4394) Seleccionar

Considera las rectas

$r \equiv \frac{x-1}{2}=\frac{y+1}{m}=z \qquad \quad s \equiv \left\{ x+nz = -2 \atop y -z = -3 \right.$

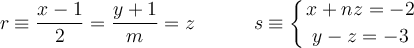
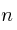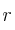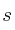– a) Halla los valores de $m$ y $n$ para los que $r$ y $s$ se cortan perpendicularmente.
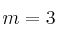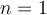– b) Para $m=3$ y $n=1$ , calcula la ecuación general del plano que contiene a 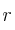$r$ y $s$
(#2746) Seleccionar

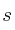
Resuelve los siguientes apartados:
– a) Calcular la ecuación del plano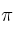 $\pi$ que pasa por 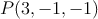$P(3,-1,-1)$ y es perpendicular a la recta
$r \equiv \left\{ x + y +z = 1 \atop 2x + y = 3 \right.$

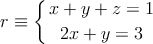
– b) Corta el plano anterior con los tres ejes de coordenadas y obtendrás tres puntos A, B y C. Calcula el Volumen del tetraedro que determinan.
(#2695) Seleccionar

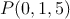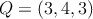Calcular la ecuación del plano que pasa por $P(0,1,5)$ y $Q=(3,4,3)$ y es paralelo a la recta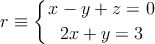 $r \equiv \left\{ x - y + z = 0 \atop 2x + y = 3 \right.$
(#4443) Seleccionar

Calcula el volumen del tetraedro ABCD y la altura del vértice B sobre la cara ACD con los siguientes datos:
$[\vec{u}, \vec{v}, \vec{w}]=3$ (producto mixto)
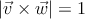$|\vec{v} \times \vec{w}|=1$ (módulo de producto vectorial)
$\vec{AB} = \vec{u}-\vec{v}$
$\vec{AC} = \vec{w}$
$\vec{AD} = \vec{w}+2\vec{v}$
(#4476) Seleccionar

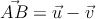
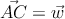
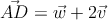
Dado el punto 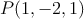$P(1,-2,1)$ , el plano 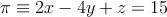$\pi \equiv 2x-4y+z=15$ y la recta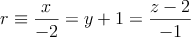 $r \equiv \frac{x}{-2}=y+1=\frac{z-2}{-1}$

a) Halla la ecuación del plano que pasa por P y contiene a r
b) Halla la ecuación de la recta que pasa por P, es paralela a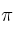 $\pi$ y corta a r