-
Determina una matriz  simétrica (
simétrica ( coincide con su traspuesta) sabiendo que
coincide con su traspuesta) sabiendo que
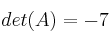
 y
y 
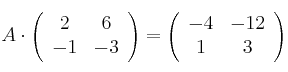
-
Considera el siguiente sistema de ecuaciones
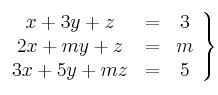
– a) Determina, si es posible, un valor de  para que el correspondiente sistema tenga una y sólo una solución.
para que el correspondiente sistema tenga una y sólo una solución.
– b) Determina, si es posible, un valor de  para que el correspondiente sistema tenga al menos dos soluciones.
para que el correspondiente sistema tenga al menos dos soluciones.
– c) Determina, si es posible, un valor de  para que el correspondiente sistema no tenga solución.
para que el correspondiente sistema no tenga solución.
-
Considera la matriz
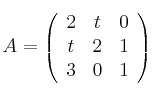
Calcula los valores de 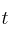 para los que el determinante de A es positivo y halla el mayor valor que alcanza dicho determinante.
para los que el determinante de A es positivo y halla el mayor valor que alcanza dicho determinante.
-
Considera la matriz
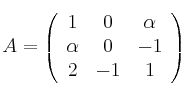
– a) Halla los valores de 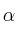 para los que la matriz
para los que la matriz  tiene inversa.
tiene inversa.
– B) Calcula, si es posible, la inversa de la matriz 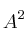 para
para 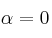
-
Considera las matrices
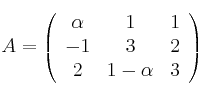
,
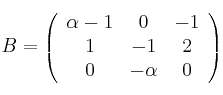
,
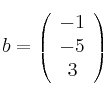
,
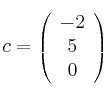
,
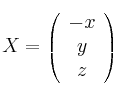
Determina 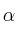 , si es posible, para que los sistemas de ecuaciones (dados en forma matricial)
, si es posible, para que los sistemas de ecuaciones (dados en forma matricial)
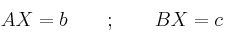
tengan infinitas soluciones (cada uno de ellos).
 andalucía
andalucía aragón
aragón asturias
asturias cantabria
cantabria castilla_leon
castilla_leon castilla_mancha
castilla_mancha catalunya
catalunya madrid
madrid MatemáticasII_Andalucía_2001
MatemáticasII_Andalucía_2001 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003 MatemáticasII_Andalucía_2004
MatemáticasII_Andalucía_2004 MatemáticasII_Andalucía_2005
MatemáticasII_Andalucía_2005 MatemáticasII_Andalucía_2006
MatemáticasII_Andalucía_2006 MatemáticasII_Andalucía_2007
MatemáticasII_Andalucía_2007 MatemáticasII_Andalucía_2008
MatemáticasII_Andalucía_2008 MatemáticasII_Andalucía_2009
MatemáticasII_Andalucía_2009 MatemáticasII_Andalucía_2010
MatemáticasII_Andalucía_2010 MatematicasII_Andalucía_2011
MatematicasII_Andalucía_2011 MatemáticasII_Andalucía_2012
MatemáticasII_Andalucía_2012 Matemáticas IES
Matemáticas IES
 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002