-
a) Plantee, sin resolver, las restricciones de este problema e indique la función a optimizar:
"Un ganadero alimenta a sus ovejas con maíz y pienso. Cada kilogramo de maíz aporta 600 g de hidratos de carbono y 200 g de proteínas, mientras que cada kilogramo de pienso aporta 300 g de hidratos de carbono y 600 g de proteínas. Cada oveja necesita diariamente como mínimo 1800 g de hidratos de carbono y 2400 g de proteínas. Si 1 kg de maíz cuesta 0.50 euros y 1 kg de pienso cuesta 0.25 euros, calcule cuántos kilogramos de cada producto tendría que comprar el ganadero para alimentar cada día a una oveja con un gasto mínimo".
b) Represente el recinto limitado por las siguientes restricciones, calculando sus vértices
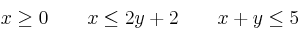
Calcule el máximo de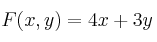 
en ese recinto, así como el punto donde se alcanza
.
-
Se quiere estimar la proporción de estudiantes que asiste de forma regular al cine. Para ello, se toma una muestra aleatoria simple de tamaño 300 y se obtiene que de ellos, 210 acuden con regularidad al cine.
– a) Calcule un intervalo de confianza al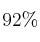 
para estimar la proporción de estudiantes que va al cine regularmente. ¿Qué error máximo se cometería si se diera como estimación de dicha proporción 0.7?
– b) Con el mismo nivel de confianza, siendo la proporción muestral la misma, si queremos que el error sea menor que 0.02, ¿cuántos alumnos como mínimo hay que elegir en la muestra?
-
Una cadena de supermercados desea estimar la proporción de clientes que adquiere un determinado producto. Para ello ha tomado una muestra aleatoria simple de 1000 clientes y ha observado que 300 compraban ese producto.
– a) Halle, con un nivel de confianza del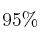 
, un intervalo de confianza para estimar la proporción de clientes del supermercado que compra ese producto.
– b) Si en otra muestra la proporción de clientes que compra ese producto es de 0.25 y el error cometido en la estimación ha sido inferior a 0.03, con un nivel de confianza del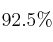 
, calcule el tamaño mínimo de la muestra.
Matemáticas IES
Matemat_Soc_Andalucia_2018
andalucía