-
En una determinada población residen 5000 personas en el centro y 10000 en la periferia. Se sabe que el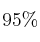 
de los residentes en el centro y que el 
de los que viven en la periferia opina que el Ayuntamiento debería restringir el acceso de vehículos privados al centro urbano. Se elige al azar un residente de la población.
a) ¿Cuál es la probabilidad de que esté a favor de restringir el acceso de vehículos privados al centro de la ciudad?
b) ¿Cuál es la probabilidad de que resida en el centro y esté a favor de la restricción de acceso?
c) Si la persona elegida opina que se debería restringir el acceso, ¿cuál es la probabilidad de que resida en el centro de la ciudad?
-
Se considera la función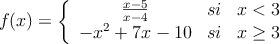 
– a) Estudie la continuidad y la derivabilidad de la función 
– b) Calcule los puntos de corte de la gráfica de con los ejes de coordenadas.
– c) Calcule las asíntotas de , en caso de que existan.
-
El consumo de cereales en una ciudad, en miles de toneladas, viene dado por la función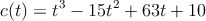 
, para 
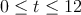, donde 
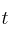representa el tiempo.
– a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
– b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
– c) Represente gráficamente la función.
-
– a) Calcule la derivada de las funciones
– b) Obtenga la ecuación de la recta tangente a la gráfica de la función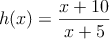 
, el punto de abscisa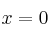 
-
El beneficio, en miles de euros, que ha obtenido una almazara a lo largo de 50 años de vida viene dado por la expresión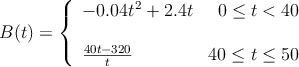 
donde 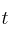es el tiempo transcurrido.
– a) Estudie la continuidad y la derivabilidad de la función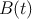 
en el intervalo ![[0,50]](local/cache-TeX/99551ec2a731e6cc48cbec9785021fd1.png "[0,50]")
.
– b) Estudie la monotonía de la función 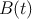y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
– c) Represente la gráfica de la función y explique la evolución del beneficio.
Matemáticas IES
Matemat_Soc_Andalucia_2018
andalucía