(66) ejercicios de Matemáticas II - Álgebra (Matrices, Determinantes y Sistemas)
-
(#3526) - Selectividad Andalucía 2011-4-A3

Considera el sistema de ecuaciones
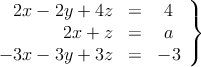
– a) Discútelo según los valores del parámetro

– b) Resuélvelo cuando sea posible -
Sean las matrices
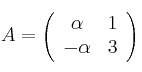
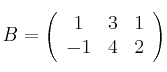
– a) Calcula los valores de
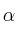 para los que la matriz inversa de A es
para los que la matriz inversa de A es 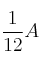
– b) Para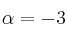 , determina la matriz
, determina la matriz 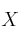 que verifica la ecuación
que verifica la ecuación 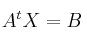 , siendo
, siendo 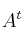 la matriz traspuesta de
la matriz traspuesta de  .
.
-
Dadas las matrices
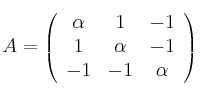
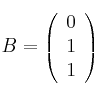
– a) Calcula el rango de
 dependiendo de los valores de
dependiendo de los valores de 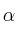
– b) Para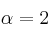 , resuelve la ecuación matricial
, resuelve la ecuación matricial 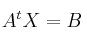
-
(#3433) - Selectividad Andalucía 2011-1-A3

Considera las matrices:
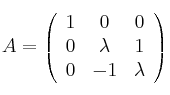
 y
y 
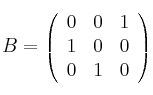
– a) ¿Hay algún valor de
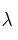 para el que
para el que  no tiene inversa?
no tiene inversa?
– b) Para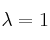 , resuelve la ecuación matricial
, resuelve la ecuación matricial 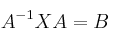
-
(#3287) - Selectividad Andalucía 2010-5-B3

Sean las matrices
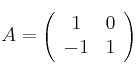
,
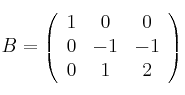
y
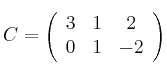
Calcula la matriz
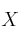 que cumpla la ecuación
que cumpla la ecuación 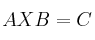
 Matemáticas IES
Matemáticas IES