-
(#3074) - Selectividad Andalucía 2008-6-B4

Considera los puntos
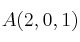 ,
, 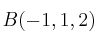 ,
, 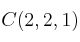 y
y 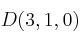 .
.– (a) Calcula la ecuación del plano
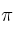 que contiene a los puntos
que contiene a los puntos  ,
, 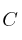 y
y 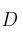
– (b) Halla el punto simétrico de respecto del plano
respecto del plano 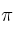 .
. -
(#3070) - Selectividad Andalucía 2008-6-A4

Se considera la recta
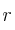 definida por
definida por 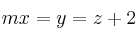 ,
, 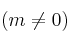 , y la recta
, y la recta 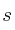 definida por
definida por 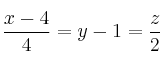
– (a) Halla el valor de
 para el que
para el que 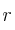 y
y 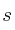 son perpendiculares.
son perpendiculares.
– (b) Deduce razonadamente si existe algún valor de para el que
para el que 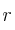 y
y 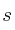 son paralelas.
son paralelas. -
(#3060) - Selectividad Andalucía 2005-5-B4

Se sabe que las rectas:
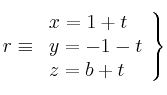
y
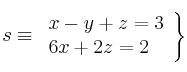
están contenidas en un mismo plano– (a) Calcula
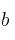
– (b) Halla la ecuación del plano que contiene a las rectas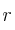 y
y 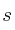
-
(#3058) - Selectividad Andalucía 2005-5-A4b

Considera el punto
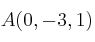 , el plano
, el plano 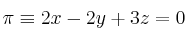 y la recta
y la recta 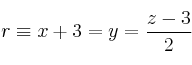 .
.– (a) Determina la ecuación del plano que pasa por
 y contiene a
y contiene a 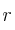 .
.
– (b) Determina la ecuación de la recta que pasa por , es paralela a
, es paralela a 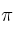 y corta a
y corta a 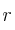 .
. -
(#3057) - Selectividad Andalucía 2005-5-A4a

Considera el punto
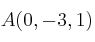 , el plano
, el plano 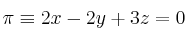 y la recta
y la recta 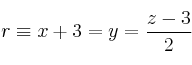 .
.– (a) Determina la ecuación del plano que pasa por
 y contiene a
y contiene a 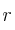 .
.
– (b) Determina la ecuación de la recta que pasa por , es paralela a
, es paralela a 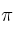 y corta a
y corta a 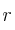 .
.
(245) ejercicios de Matemáticas PAU Andalucía
(32) ejercicios de Matemáticas II - Geometría (Geometría en el espacio)
 Matemáticas IES
Matemáticas IES