Ejercicios de Geometría - 1º Bach. Ciencias

(87) ejercicios de Geometría en el Plano

(#4095) Seleccionar

Dado el vector 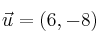$\vec{u}=(6,-8)$ hallar:

– Los vectores unitarios con la misma dirección de $\vec{u}$
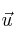
– Los vectores ortogonales a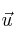 $\vec{u}$ con el mismo módulo que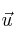 $\vec{u}$
– Los vectores unitarios y ortogonales a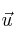 $\vec{u}$
(#4160) Seleccionar

Halla la ecuación de una recta que pase por el (0,0) y que sea perpendicular a la recta que pasa por A(1,1) y B(2,2)
(#4161) Seleccionar

Halla el valor de todos los ángulos del rombo cuyos vértices son: A(1, 0) , B(3, 4) , C(5, 0) y D(3, -4)
(#1413) Seleccionar

Sean L1 y L2 las rectas de ecuación

$L1 \longrightarrow (c+1)x - 4y - (c-1) = 0$
$L2 \longrightarrow y= \frac{-1}{3} x + 1$

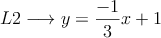
donde $c \in R$

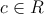
a) Determinar el valor de c para el cual la recta L1 ea perpendicular a la recta L2. Escribir la ecuación de la recta L1

b) Hallar analíticamente el punto de intersección de las rectas L1 y L2 y verificar gráficamente el resultado hallado.

c) Encontrar la ecuación de la recta L que es paralela a la recta L1 y pasa por el punto P= ( -1/3 , 1/3)
(#3700) Seleccionar

Un explorador queda atrapado en una tormenta de nieve (en el que la nevada es tan espesa que el suelo no se puede distinguir del cielo) mientras regresa al campamento base. Se suponía que debía viajar al norte por 5,89 km, pero cuando la nieve se despeja, descubre que en realidad viajó 7,51 km a 59,0° al norte del este. Presente el procedimiento paso a paso y con base en la anterior información responda las siguientes preguntas:
(a) ¿Qué tanto debe caminar para volver al campamento base?
(b) ¿en qué dirección debe viajar ahora para llegar al campamento base? NOTA: presente su respuesta con respecto al semieje positivo horizontal.