Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
– Despeja la matriz
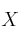 en función de
en función de  e
e 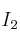 en la ecuación
en la ecuación 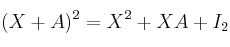 , siendo
, siendo 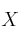 y
y  matrices cuadradas de orden dos, e
matrices cuadradas de orden dos, e 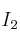 la matriz identidad de orden 2.
la matriz identidad de orden 2.
– Resuelve la ecuación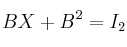 siendo
siendo
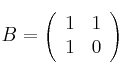
e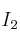 la matriz identidad de orden 2.
la matriz identidad de orden 2.
-
Hállense las matrices
 cuadradas de orden 2, que verifican la igualdad:
cuadradas de orden 2, que verifican la igualdad:
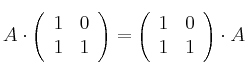
-
Dadas las matrices
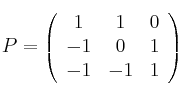
y
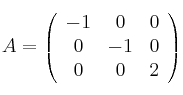
hállese razonadamente la matriz
 sabiendo que
sabiendo que 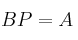
-
Considera el sistema de ecuaciones
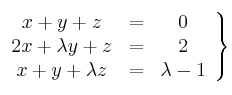
– a) Determina el valor de
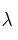 para que el sistema sea incompatible.
para que el sistema sea incompatible.
– b) Resuelva el sistema para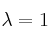
-
Discute el siguiente sistema en función de los valores del parámetro

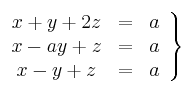
 Matemáticas IES
Matemáticas IES
