Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
Discute el siguiente sistema en función de los valores del parámetro

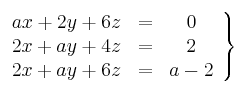
-
Considera la matriz
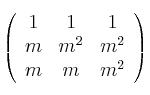
– a) Halla los valores del parámetro
 para los que el rango de A es menor que 3
para los que el rango de A es menor que 3
– b) Estudia si el sistema
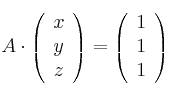 tiene solución para cada uno de los valores de m obtenidos en el apartado anterior.
tiene solución para cada uno de los valores de m obtenidos en el apartado anterior.
-
Álvaro, Marta y Guillermo son tres hermanos. Álvaro dice a Marta: si te doy la quinta parte del dinero que tengo, los tres hermanos tendremos la misma cantidad. Calcula lo que tiene cada uno si entre los tres juntan 84 euros.
-
Considera el sistema de ecuaciones:
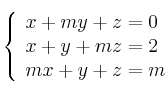
– (a) ¿Para qué valor de
 el sistema tiene al menos dos soluciones?
el sistema tiene al menos dos soluciones?
– (b) ¿Para qué valores de el sistema admite solución en la que
el sistema admite solución en la que 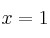 ?
? -
Considera el sistema de ecuaciones:
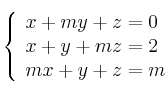
– (a) ¿Para qué valor de
 el sistema tiene al menos dos soluciones?
el sistema tiene al menos dos soluciones?
– (b) ¿Para qué valores de el sistema admite solución en la que
el sistema admite solución en la que 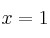 ?
?
 Matemáticas IES
Matemáticas IES

