Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
(a) Se sabe que el determinante de una matriz cuadrada
 de orden 3 vale
de orden 3 vale 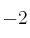 ¿Cuánto vale el determinante de la matriz
¿Cuánto vale el determinante de la matriz 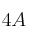 ?
?(b) Dada la matriz
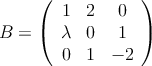
, ¿para qué valores de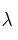 la matriz
la matriz 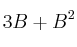 no tiene inversa?
no tiene inversa? -
Dadas las matrices
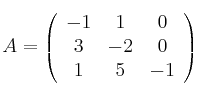
y
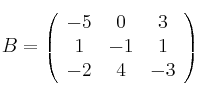
halla la matriz
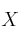 que cumple
que cumple 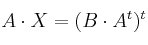
-
Dada la matriz
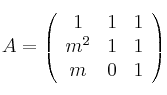
, se pide:– (a) Determina los valores de
 para los que la matriz
para los que la matriz  tiene inversa.
tiene inversa.
– (b) Calcula, si es posible la matriz inversa de para
para 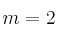
-
Sean
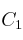 ,
, 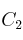 y
y 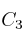 las columnas primera, segunda y tercera, respectivamente, de una matriz cuadrada
las columnas primera, segunda y tercera, respectivamente, de una matriz cuadrada  de orden 3 cuyo determinante vale 5. Calcula, indicando las propiedades que utilices:
de orden 3 cuyo determinante vale 5. Calcula, indicando las propiedades que utilices:
– (a) El determinante de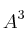 .
.
– (b) El determinante de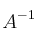 .
.
– (c) El determinante de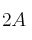 .
.
– (d) El determinante de una matriz cuadrada cuyas columnas primera, segunda y tercera son, respectivamente,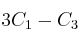 ,
, 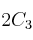 y
y 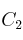 .
. -
Considera el sistema de ecuaciones
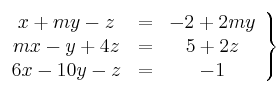
– (a) Discute las soluciones del sistema según los valores de

– (b) Resuelve el sistema cuando sea compatible indeterminado.
 Matemáticas IES
Matemáticas IES