Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
Considera la matriz
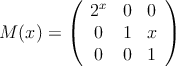
(a) ¿Para qué valores de
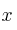 existe
existe 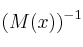 ?. Para los valores de
?. Para los valores de 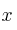 obtenidos, calcula la matriz
obtenidos, calcula la matriz 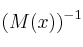 .
.(b) Resuelve, si es posible, la ecuación
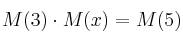 .
. -
Considera las matrices
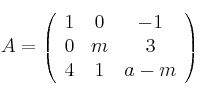 ,
,
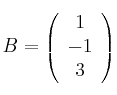 y
y
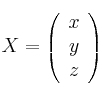
– (a) ¿Para qué valores de
 existe la matriz
existe la matriz 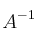 ?
?
– (b) Siendo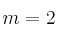 , calcula
, calcula 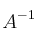 y resuelve el sistema
y resuelve el sistema 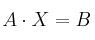
– (c) Resuelve el sistema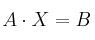 para
para 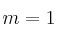
-
Una empresa cinematográfica dispone de tres salas, A, B y C. Los precios de entrada a estas salas son de 3, 4 y 5 euros, respectivamente. Un día la recaudación conjunta de las tres salas fue de 720 euros y el número total de espectadores fue de 200. Si los espectadores de la sala A hubiesen asistido a la sala B y los de la sala B a la sala A, se hubiese obtenido una recaudación de 20 euros más. Calcula el número de espectadores que acudió a cada una de las salas.
-
Se sabe que el sistema de ecuaciones
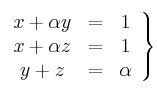
tiene una única solución.
– (a) Prueba que
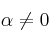
– (b) Halla las soluciones del sistema -
Sabiendo que
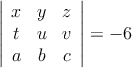 ,
,calcula, indicando las propiedades que utilices, los siguientes determinantes:
(a)
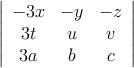
(b)
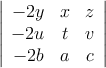
(c)
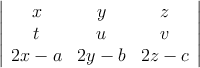
 Matemáticas IES
Matemáticas IES