Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias

(110) ejercicios de Matrices, Determinantes y Sistemas

(#3227)
Seleccionar

Considera el sistema de ecuaciones
$\left. \begin{array}{lcl} x-my+z & = & 1 \\ x+y+z & = & m+2 \\ x+y+mz & = &4 \end{array} \right\}$

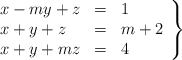
– a) Clasifícalo según los valores del parámetro $m$
– b) Resuélvelo cuando sea compatible indeterminado
(#3228)
Seleccionar

Sin desarrollarlo, calcula el valor del determinante de la matriz

$A = \left( \begin{array}{ccc} 1 & 3 & k\\ k & 1 & 3\\ 1 & 7 & k \end{array} \right)$

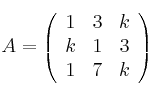
y enuncia las propiedades que hayas usado
(#3238)
Seleccionar

Considera las matrices

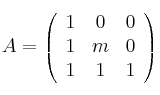
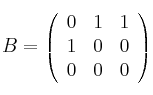
$A = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 1 & m & 0 \\ 1 & 1 & 1 \end{array} \right)$
,
$B = \left( \begin{array}{ccc} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)$
y
$C = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right)$

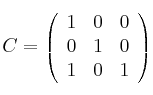
– (a) ¿Para qué valores de $m$ tiene solución la ecuación matricial $A \cdot X + 2B = 3C$ ?
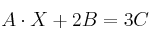– (b) Resuelve la ecuación matricial dada para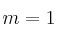 $m=1$
(#3239)
Seleccionar

Considera las matrices
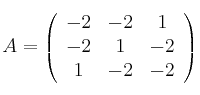
$A = \left( \begin{array}{ccc} -2 & -2 & 1 \\ -2 & 1 & -2 \\ 1 & -2 & -2 \end{array} \right)$
y
$X = \left( \begin{array}{c} x \\ y \\ z \end{array} \right)$

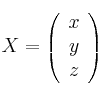
– (a) Siendo 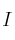$I$ la matriz identidad de orden 3, calcula los valores de 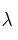$\lambda$ para los que la matriz 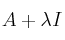$A+\lambda I$ no tiene inversa.
– (b) Resuelve el sistema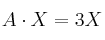 $A \cdot X = 3X$ e interpreta geométricamente el conjunto de todas sus soluciones.
(#3240)
Seleccionar

Determina razonadamente los valores de $m$ para los que el sistema de ecuaciones
$\left. \begin{array}{ccc} 2x+y+ z & = & mx \\ x + 2y+ z & = & my \\ x + 2y+ 4z & = & mz \end{array} \right\}$

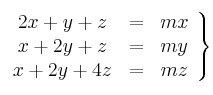
tiene más de una solución

Matemáticas IES

Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias

(110) ejercicios de Matrices, Determinantes y Sistemas

Ejercicios Seleccionados