Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
Considera el siguiente sistema de ecuaciones
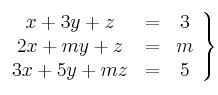
– a) Determina, si es posible, un valor de
 para que el correspondiente sistema tenga una y sólo una solución.
para que el correspondiente sistema tenga una y sólo una solución.
– b) Determina, si es posible, un valor de para que el correspondiente sistema tenga al menos dos soluciones.
para que el correspondiente sistema tenga al menos dos soluciones.
– c) Determina, si es posible, un valor de para que el correspondiente sistema no tenga solución.
para que el correspondiente sistema no tenga solución. -
Determina una matriz
 simétrica (
simétrica ( coincide con su traspuesta) sabiendo que
coincide con su traspuesta) sabiendo que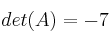
 y
y 
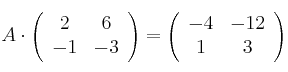
-
Determina la matriz
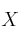 que verifica la ecuación
que verifica la ecuación 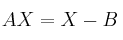 siendo
siendo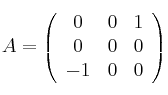
 y
y 
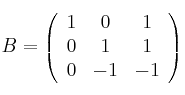
-
Considera
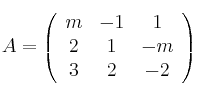
 ,
, 
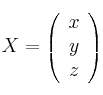
 y
y 
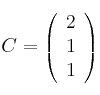
– a) ¿Para qué valores de
 tiene inversa la matriz
tiene inversa la matriz  ?
?
– b) Resuelve, para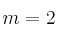 , el sistema de ecuaciones
, el sistema de ecuaciones 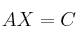
-
Denotamos por
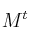 a la matriz traspuesta de una matriz
a la matriz traspuesta de una matriz 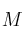 . Considera
. Considera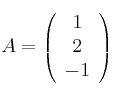
 ,
, 
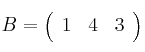
 y
y 
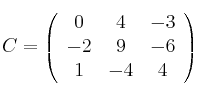
– a) Calcula
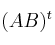 y
y 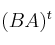
– b) Determina una matriz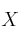 que verifique la relación
que verifique la relación 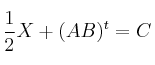
 Matemáticas IES
Matemáticas IES

