-
En un sistema de alarma, la probabilidad de que haya un incidente es 0.1. Si éste se produce, la probabilidad de que la alarma suene es 0.95. La probabilidad de que suene la alarma sin que haya incidente es de 0.03.
– a) ¿Cuál es la probabilidad de que suene la alarma?
– b) Si ha sonado la alarma, calcule la probabilidad de que no haya habido incidente.
-
Sean  y
y  dos sucesos aleatorios tales que:
dos sucesos aleatorios tales que:
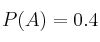 ,
, 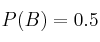 y
y 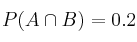
– a) Calcule razonadamente las probabilidades 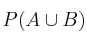 ,
, 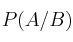 y
y 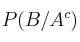
– b) Razone si  y
y  son sucesos incompatibles.
son sucesos incompatibles.
– c) Razone si  y
y  son independientes
son independientes
-
En una capital se editan dos periódicos, CIUDAD y LA MAÑANA. Se sabe que el 85%
de la población lee alguno de ellos, que el 18% lee los dos y que el 70% lee CIUDAD.
Si elegimos al azar un habitante de esa capital, halle la probabilidad de que:
– a) No lea ninguno de los dos.
– b) Lea sólo LA MAÑANA.
– c) Lea CIUDAD, sabiendo que no lee LA MAÑANA.
-
En el experimento aleatorio consistente en lanzar un dado equilibrado con las caras numeradas del 1 al 6 y observar el resultado se consideran los siguientes sucesos: A: “obtener un número mayor que 4”, B: “obtener un número par”.
a) Escriba los elementos de cada uno de los siguientes sucesos:
 ;
;  ;
; 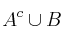 ;
; 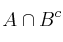 ;
; 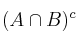
b) Calcule las probabilidades 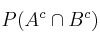 y
y 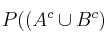
-
Lanzamos un dado, si sale 5 o 6 extraemos una bola de una urna A, que contiene 6 bolas
blancas y 4 negras. Si sale otro resultado se extrae una bola de la urna B, que contiene 3
bolas blancas y 7 negras. Calcule:
– a) La probabilidad de que la bola extraída sea negra.
– b) La probabilidad de que la bola sea negra y de la urna B.
– c) La probabilidad de que haya salido menos de 5 si la bola extraída ha sido blanca.