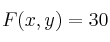-
Un Ayuntamiento concede licencia para la construcción de una urbanización de a lo sumo 120 viviendas, de dos tipos A y B.
Para ello la empresa constructora dispone de un capital máximo de 15 millones de euros, siendo el coste de construcción de la vivienda de tipo A de 100000 euros y la de tipo B 300000 euros.
Si el beneficio obtenido por la venta de una vivienda de tipo A asciende a 20000 euros y por una de tipo B a 40000 euros, ¿cuántas viviendas de cada tipo deben construirse para obtener un beneficio máximo?
-
(a) Represente la región definida por las siguientes inecuaciones y determine sus vértices:
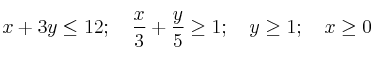
(b) Calcule los valores extremos de la función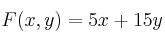 
en dicha región y dónde se alcanzan.
-
En un examen de Matemáticas se propone el siguiente problema:
"Indique dónde se alcanza el mínimo de la función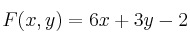 
en la región determinada por las restricciones 
; 
; 
."
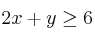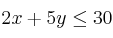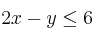– (a) Resuelva el problema
– (b) Ana responde que se alcanza en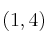 
y Benito que lo hace en 
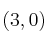. ¿Es cierto que el mínimo se alcanza en 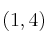?. ¿Es cierto que se alcanza en ?.
-
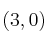Una empresa produce botellas de leche entera y de leche desnatada y tiene una capacidad de producción máxima de 6000 botellas al día. Las condiciones de la empresa obligan a que la producción de botellas de leche desnatada sea, al menos, la quinta parte de las de leche entera y, como máximo, el triple de la misma. El beneficio de la empresa por botella de leche entera es de 20 céntimos y por botella de leche desnatada es de 32 céntimos. Suponiendo que se vende toda la producción, determine la cantidad de botellas de cada tipo que proporciona un beneficio máximo y el importe de este beneficio.
-
Se considera el recinto R del plano, determinado por las siguientes inecuaciones:
, 
, 
, 
, 
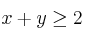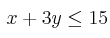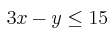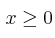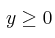
– (a) Represente gráficamente el recinto R y calcule sus vértices
– (b) Halle los valores máximo y mínimo que alcanza la función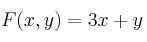 
en dicho recinto
– (c) Razone si existen puntos (x,y) del recinto, para los que 
