Ejercicios de Matemáticas Aplicadas a las Ciencias Sociales II (2º Bachillerato)

(28) ejercicios de Programación Lineal

(#3316) Seleccionar

Desde dos almacenes A y B, se tiene que distribuir fruta a tres mercados de la ciudad. El almacén A dispone de 10 toneladas de fruta diarias y el B de 15 toneladas, que se reparten en su totalidad. Los dos primeros mercados necesitan, diariamente, 8 toneladas de fruta, mientras que el tercero necesita 9 toneladas diarias.
El coste del transporte desde cada almacén a cada mercado viene dado por el siguiente cuadro:

Planificar el transporte para que el coste sea mínimo.
(#3279) Seleccionar

(a) Represente gráficamente la región determinada por las siguientes restricciones:

$2x+y \le 6 ; \quad 4x+y \le 10 ; \quad -x+y \le 3 ; \quad x \ge 0 ; \quad y \ge 0$

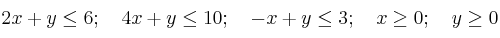
(b) Calcule el máximo de la función 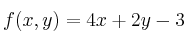$f(x,y) = 4x+2y-3$ en el recinto anterior e indique dónde se alcanza.
(#3272) Seleccionar

Consideramos el recinto del plano limitado por las siguientes inecuaciones:

$y-x \le 4 ; \quad y+2x \ge 7 ; \quad -2x-y+13 \ge 0 ; \quad x \ge 0 ; \quad y \ge 0$

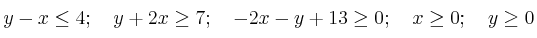
(a) Represente el recinto y calcule sus vértices.
(b) Halle en qué puntos de ese recinto alcanza los valores máximo y mínimo la función $F(x,y)=4x+2y-1$
(#3370) Seleccionar

Sea el recinto definido por el siguiente sistema de inecuaciones:
$3x+y \ge 4$ ; $x+y\le 6$ ; $0\le y \le 5$

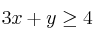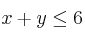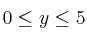
a) Represéntelo gráficamente
b) Calcule los vértices de dicho recinto
c) En el recinto anterior, halle los valores máximo y mínimo de la función 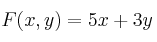$F(x,y)=5x+3y$ . ¿En qué puntos se alcanzan dichos valores?
(#3403) Seleccionar

a) Dibuje el recinto del plano definido por las inecuaciones:
$x+3y \ge 9$ ; $4x-5y+25 \ge 0$ ; $7x-2y\le 17$ ; $x \ge 0$ ; $y \ge 0$
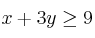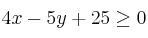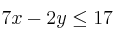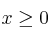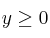
b) Calcule los vértices del mismo
c) Obtenga en dicho recinto los valores máximo y mínimo de la función 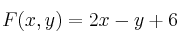$F(x,y) = 2x-y+6$ y los puntos donde se alcanzan.