-
Sea la función 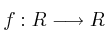 definida por:
definida por:
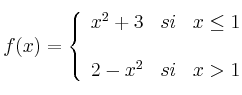
– (a) Calcula, si es posible, las derivadas laterales de  en
en 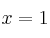
– (b) Halla los intervalos de crecimiento y de decrecimiento de la función 
-
Sea 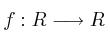 definida por
definida por ![f (x) = \sqrt[3]{x} f (x) = \sqrt[3]{x}](local/cache-TeX/b62b7b1bfd3ad59587dd967979d5d1a8.png)
– (a) Calcula la recta tangente a la gráfica de f en el punto de abscisa 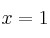 .
.
– (b) Esboza el recinto limitado por la gráfica de f y la recta tangente obtenida.
– (c) Calcula el área del recinto descrito en el apartado anterior.
-
Sea 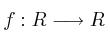 definida por
definida por ![f (x) = \sqrt[3]{x} f (x) = \sqrt[3]{x}](local/cache-TeX/b62b7b1bfd3ad59587dd967979d5d1a8.png)
– (a) Calcula la recta tangente a la gráfica de f en el punto de abscisa 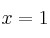 .
.
– (b) Esboza el recinto limitado por la gráfica de f y la recta tangente obtenida.
– (c) Calcula el área del recinto descrito en el apartado anterior.
-
Considera la función 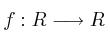 definida por
definida por 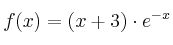
– (a) Halla las asíntotas de la gráfica de f
– (b) Determina los extremos relativos de f y los puntos de inflexión de su gráfica
– (c) Esboza la gráfica de f
-
Dadas la parábola de ecuación 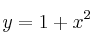 y la recta de ecuación
y la recta de ecuación 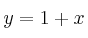 , se pide:
, se pide:
– (a) Área de la región limitada por la recta y la parábola.
– (b) Ecuación de la recta paralela a la dada que es tangente a la parábola.
 andalucía
andalucía aragón
aragón asturias
asturias cantabria
cantabria castilla_leon
castilla_leon castilla_mancha
castilla_mancha catalunya
catalunya madrid
madrid MatemáticasII_Andalucía_2001
MatemáticasII_Andalucía_2001 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003 MatemáticasII_Andalucía_2004
MatemáticasII_Andalucía_2004 MatemáticasII_Andalucía_2005
MatemáticasII_Andalucía_2005 MatemáticasII_Andalucía_2006
MatemáticasII_Andalucía_2006 MatemáticasII_Andalucía_2007
MatemáticasII_Andalucía_2007 MatemáticasII_Andalucía_2008
MatemáticasII_Andalucía_2008 MatemáticasII_Andalucía_2009
MatemáticasII_Andalucía_2009 MatemáticasII_Andalucía_2010
MatemáticasII_Andalucía_2010 MatematicasII_Andalucía_2011
MatematicasII_Andalucía_2011 MatemáticasII_Andalucía_2012
MatemáticasII_Andalucía_2012 Matemáticas IES
Matemáticas IES
 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003