-
Un índice para calibrar la madurez lectora de los alumnos de primaria se distribuye
según una ley Normal con desviación típica 2. Elegida una muestra de 18 alumnos en un centro de primaria, se obtiene una media muestral de 10.8 en dicho índice. Mediante el uso de un contraste de hipótesis, ¿se puede aceptar, con un nivel de significación del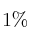 
, la hipótesis nula de que la media del índice de madurez lectora de los alumnos de este centro no es inferior a 11?
-
Se cree que al menos el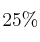 
de los usuarios de teléfonos móviles son de
contrato. De una encuesta realizada a 950 personas, elegida al azar, 200 de ellas
manifestaron que tenían teléfono móvil de contrato. A la vista de estos resultados y con
un nivel de significación del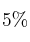 
, ¿puede admitirse que la proporción de personas con
contrato en su teléfono móvil ha disminuido? Utilice para la resolución del problema un
contraste de hipótesis con hipótesis nula “la proporción p es mayor o igual que 0.25”.
-
Un informe de un Ayuntamiento afirma que al menos el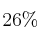 
de los usuarios del carril bici habrían utilizado el coche particular para sus desplazamientos de no haber existido dicho carril. Sin embargo, un periódico local anuncia la falsedad del dato, informando que una encuesta propia indica que solo 240 de los 1000 usuarios encuestados afirman que habrían utilizado el coche particular.
– a) Establezca un contraste, con hipótesis nula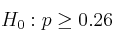 
, para verificar la afirmación del Ayuntamiento e indique la región crítica de dicho contraste para un nivel de significación del .
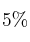– b) Con este nivel de significación ¿podría aceptarse el informe del Ayuntamiento?
-
En el mar hay una mancha producida por una erupción marina. La superficie afectada, en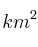 
, viene dada por la función 
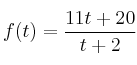, siendo 
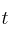el tiempo transcurrido desde que empezamos a observarla.
– a) ¿Cuál es la superficie afectada inicialmente, cuando empezamos a medirla?
– b) Estudie si la mancha crece o decrece con el tiempo
– c) ¿Tiene algún límite la extensión de la superficie de la mancha?
-
Sea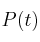 
el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo 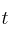, medido en meses:
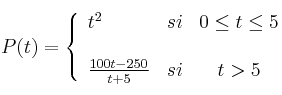
– a) Estudie la continuidad de la función P.
– b) Estudie la derivabilidad de P en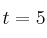 
.
– c) Estudie la monotonía de dicha función e interprete la evolución del porcentaje de células afectadas.
– d) ¿En algún momento el porcentaje de células afectadas podría valer 50?
Matemáticas IES
Matemat_Soc_Andalucía_2012
andalucía