-
(#4006) - Selectividad Andalucía 2014-2-A1

– a) Represente gráficamente la región definida por las siguientes inecuaciones y calcule sus vértices
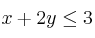 ;
; 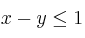 ;
; 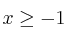 ;
; 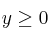
– b) Calcule los valores máximo y mínimo de la función objetivo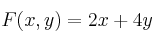 en la región anterior y los puntos donde se alcanzan.
en la región anterior y los puntos donde se alcanzan. -
(#3904) - Selectividad Andalucía 2013-2-A1

Sea
 la región factible definida por las siguientes inecuaciones
la región factible definida por las siguientes inecuaciones 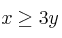 ,
, 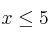 ,
, 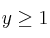 .
. – a) (0.5 puntos) Razone si el punto
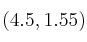 pertenece a
pertenece a 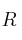 .
.
– b) (1.5 puntos) Dada la función objetivo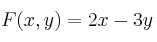 , calcule sus valores extremos en
, calcule sus valores extremos en 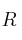 .
.
– c) (0.5 puntos) Razone si hay algún punto de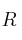 donde la función
donde la función 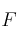 valga
valga 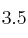 . ¿Y
. ¿Y 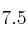 ?
? -
(#3301) - Selectividad Andalucía 2011-5-A1

Se considera el recinto R del plano, determinado por las siguientes inecuaciones:
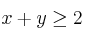 ,
, 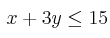 ,
, 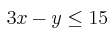 ,
, 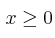 ,
, 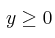
– (a) Represente gráficamente el recinto R y calcule sus vértices
– (b) Halle los valores máximo y mínimo que alcanza la función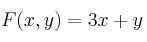 en dicho recinto
en dicho recinto
– (c) Razone si existen puntos (x,y) del recinto, para los que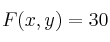
-
(#3403) - Selectividad Andalucía 2010-6-B1

a) Dibuje el recinto del plano definido por las inecuaciones:
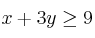 ;
; 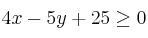 ;
; 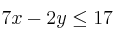 ;
; 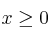 ;
; 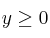
b) Calcule los vértices del mismo
c) Obtenga en dicho recinto los valores máximo y mínimo de la función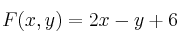 y los puntos donde se alcanzan.
y los puntos donde se alcanzan. -
(#3370) - Selectividad Andalucía 2010-3-A-1

Sea el recinto definido por el siguiente sistema de inecuaciones:
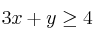 ;
; 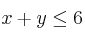 ;
; 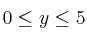
– a) Represéntelo gráficamente
– b) Calcule los vértices de dicho recinto
– c) En el recinto anterior, halle los valores máximo y mínimo de la función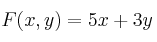 . ¿En qué puntos se alcanzan dichos valores?
. ¿En qué puntos se alcanzan dichos valores?
(245) ejercicios de Matemáticas PAU Andalucía
(19) ejercicios de Mat. C. Sociales II - Programación Lineal (Optimización, Sistemas de Inecuaciones)
 Matemáticas IES
Matemáticas IES