Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
– (a) Determina razonadamente los valores del parámetro
 para los que el siguiente sistema de ecuaciones tiene más de una solución:
para los que el siguiente sistema de ecuaciones tiene más de una solución: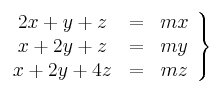
– (b) Resuelve el sistema anterior para el caso
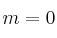 y para el caso
y para el caso 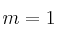 .
. -
Dada la matriz
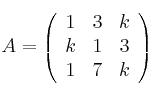
– (a) Estudia el rango de
 en función de los valores del parámetro
en función de los valores del parámetro 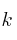 .
.
– (b) Para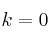 , halla la matriz inversa de
, halla la matriz inversa de  .
. -
De las matrices:
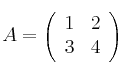 ,
,
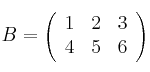 ,
,
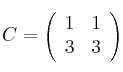 y
y
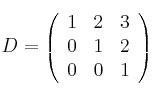
determina cuáles tienen inversa y en los casos en que exista, calcula el determinante de dichas inversas.
-
Considera
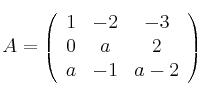 ,
,
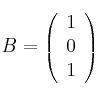 y
y
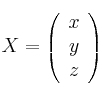
– (a) Determina el rango de
 en función del parámetro
en función del parámetro 
– (b) Discute en función de en sistema, dado en forma matricial
en sistema, dado en forma matricial 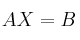
– (c) Resuelve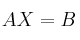 en los casos en que sea compatible indeterminado.
en los casos en que sea compatible indeterminado. -
Sea

¿Para qué valores de
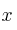 existe la matriz inversa de
existe la matriz inversa de  ?. Calcula dicha matriz inversa.
?. Calcula dicha matriz inversa.
 Matemáticas IES
Matemáticas IES

