Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
En el sector de las aceitunas sin hueso, tres empresas A, B y C, se encuentran en competencia. Calcula el precio por unidad dado por cada empresa sabiendo que verifican las siguientes relaciones:
– El precio de la empresa A es 0,6 euros menos que la media de los precios establecidos por B y C.
– El precio dado por B es la media de los precios de A y C.
– El precio de la empresa C es igual a 2 euros mas 2/5 del precio dado por A mas 1/3 del precio dado por B. -
Considera las matrices
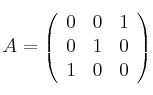
,
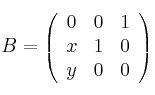
– a) Calcula la matriz inversa de

– b) Calcula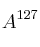 y
y 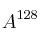
– c) Determina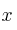 e
e 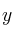 tal que
tal que 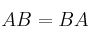
-
Considera las matrices
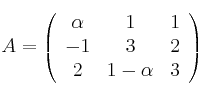
,
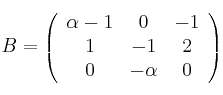
,
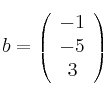
,
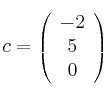
,
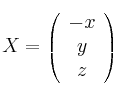
Determina
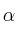 , si es posible, para que los sistemas de ecuaciones (dados en forma matricial)
, si es posible, para que los sistemas de ecuaciones (dados en forma matricial)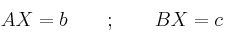
tengan infinitas soluciones (cada uno de ellos).
-
Considera la matriz
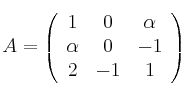
– a) Halla los valores de
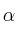 para los que la matriz
para los que la matriz  tiene inversa.
tiene inversa.
– B) Calcula, si es posible, la inversa de la matriz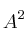 para
para 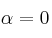
-
Considera la matriz
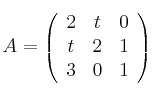
Calcula los valores de
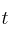 para los que el determinante de A es positivo y halla el mayor valor que alcanza dicho determinante.
para los que el determinante de A es positivo y halla el mayor valor que alcanza dicho determinante.
 Matemáticas IES
Matemáticas IES

