Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias

(110) ejercicios de Matrices, Determinantes y Sistemas

(#4357) Seleccionar

Usa la regla de Cramer para resolver el siguiente sistema de ecuaciones
$\left\{ \begin{array}{lcc} x + 2y + z = 9\\ x - y - z = -10\\ 2x - y + z = 5 \end{array} \right.$
(#4363) Seleccionar

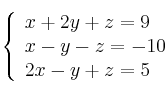
Dado el siguiente sistema:
$\left\{ \begin{array}{l} -z+2x=-1 \\ -x+2y-2=-3 \\ y+3x-5z=-12 \end{array} \right.$

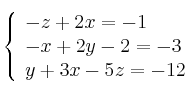
– a) Escribe la matriz de los coeficientes, la matriz ampliada, la de las incógnitas y la de los términos independientes. Expresa el sistema en forma matricial
– b) Resuelve el sistema por el método que desees (Cramer o Gauss). A la vista de las soluciones, ¿de qué tipo es el sistema?
(#3958) Seleccionar

Dadas las matrices 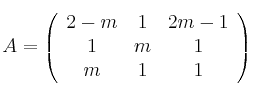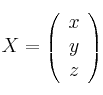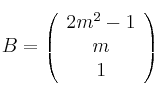$A = \left( \begin{array}{ccc} 2-m & 1 & 2m-1 \\ 1 & m & 1 \\ m & 1 & 1 \end{array} \right)$ , $X = \left( \begin{array}{c} x \\ y \\ z \end{array} \right)$ , $B = \left( \begin{array}{c} 2m^2-1 \\ m \\ 1 \end{array} \right)$ , considera el sistema de ecuaciones lineales dado por 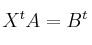$X^tA=B^t$ , donde 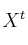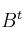$X^t$ , $B^t$ denotan las traspuestas. Discútelo según los distintos valores de m
(#3955) Seleccionar

Calcula todas las matrices 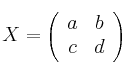$X = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)$ tales que 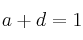$a+d=1$ , tienen determinante 1 y cumplen 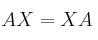$AX=XA$ , siendo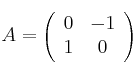 $A = \left( \begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right)$
(#4390) Seleccionar

Considera las siguientes matrices
$A=\left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & -1 & 0 \\ 1 & 0 & 0 \end{array} \right) \qquad B=\left( \begin{array}{ccc} a & b & c \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{array} \right)$

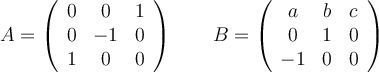
– a) Determina, si existen, los valores de a, b y c para los que las matrices A y B conmutan
– b) Calcula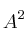 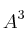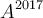$A^2$ , $A^3$ , $A^{2017}$ y $A^{2018}$
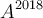
– c) Calcula, si existe, la matriz inversa de $A$