Matemáticas IES

(#3284) - Selectividad Andalucía 2009-2-A1              

(a) Represente la región definida por las siguientes inecuaciones y determine sus vértices:

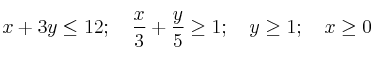
(b) Calcule los valores extremos de la función 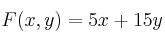en dicha región y dónde se alcanzan.

(#3283) - Selectividad Andalucía 2009-1-B1            

En un examen de Matemáticas se propone el siguiente problema:
"Indique dónde se alcanza el mínimo de la función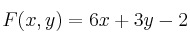 en la región determinada por las restricciones ; ; ."

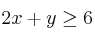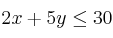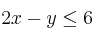– (a) Resuelva el problema
– (b) Ana responde que se alcanza en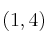 y Benito que lo hace en 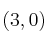. ¿Es cierto que el mínimo se alcanza en 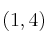?. ¿Es cierto que se alcanza en ?.

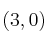(#3282) - Selectividad Andalucía 2008-6-A1              

Una empresa produce botellas de leche entera y de leche desnatada y tiene una capacidad de producción máxima de 6000 botellas al día. Las condiciones de la empresa obligan a que la producción de botellas de leche desnatada sea, al menos, la quinta parte de las de leche entera y, como máximo, el triple de la misma. El beneficio de la empresa por botella de leche entera es de 20 céntimos y por botella de leche desnatada es de 32 céntimos. Suponiendo que se vende toda la producción, determine la cantidad de botellas de cada tipo que proporciona un beneficio máximo y el importe de este beneficio.

(#3279) - Selectividad Andalucía 2008-3-B1              

(a) Represente gráficamente la región determinada por las siguientes restricciones:

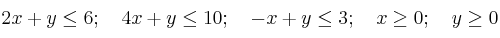
(b) Calcule el máximo de la función 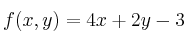en el recinto anterior e indique dónde se alcanza.

(#3272) - Selectividad Andalucía 2007-2-B1              

Consideramos el recinto del plano limitado por las siguientes inecuaciones:

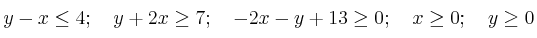
– (a) Represente el recinto y calcule sus vértices.
– (b) Halle en qué puntos de ese recinto alcanza los valores máximo y mínimo la función