Ejercicios Resueltos de Programación Lineal

(245) ejercicios de Matemáticas PAU Andalucía

(19) ejercicios de Mat. C. Sociales II - Programación Lineal (Optimización, Sistemas de Inecuaciones)

(#4377) - Selectividad Andalucía Junio 2014 B1

a) Dadas las inecuaciones
$y \leq x + 5, \qquad 2x + y \geq -4, \qquad 4x \leq 10 -y, \qquad y \geq 0$
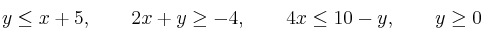
represente el recinto que limitan y calcule sus vértices.
b) (0.7 puntos) Obtenga el máximo y el mínimo de la función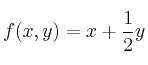 $f(x,y) =x+ \frac{1}{2}y$ en el recinto anterior, así como los puntos en los que se alcanzan.
(#4617) - Selectividad Andalucía 2021-1 A1

Un laboratorio farmacéutico tiene una línea de producción con dos medicamentos A y B, con marca comercial y genérico respectivamente, de los cuales, entre los dos como máximo puede fabricar 10 unidades a la hora. Desde el punto de vista del rendimiento, se han de producir al menos 4 unidades por hora entre los dos y por motivos de política sanitaria, la producción de A ha de ser como mucho 2 unidades más que la de B.
Cada unidad de tipo A que vende le produce un beneficio de 60 euros, mientras que cada unidad de tipo B le produce un beneficio de 25 euros. Si se vende todo lo que se produce, determine las unidades de cada medicamento que deberá fabricar por hora para maximizar su beneficio y obtenga el valor de dicho beneficio.
(#4616) - Selectividad Andalucía 2021 Julio A2

Se consideran las siguientes inecuaciones:

$5x - 4y \leq -19 \qquad 3x - 4y \leq -13 \qquad x \geq -7 \qquad -x-y \geq 2$

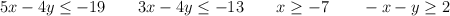
a) Represente la región factible defnida por las inecuaciones anteriores y determine sus vértices.

b) ¿Cuáles son los puntos en los que se alcanzan el mínimo y el máximo de la función
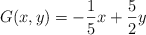$G(x, y) = -\frac{1}{5}x + \frac{5}{2}y$ en la citada región factible? ¿Cuál es su valor?.

c) Responda de forma razonada si la función 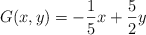$G(x, y) = -\frac{1}{5}x + \frac{5}{2}y$ puede alcanzar el valor 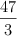$\frac{47}{3}$ en la región factible hallada.
(#4375) - Selectividad Andalucía 2018 Junio A1

a) Plantee, sin resolver, las restricciones de este problema e indique la función a optimizar:
"Un ganadero alimenta a sus ovejas con maíz y pienso. Cada kilogramo de maíz aporta 600 g de hidratos de carbono y 200 g de proteínas, mientras que cada kilogramo de pienso aporta 300 g de hidratos de carbono y 600 g de proteínas. Cada oveja necesita diariamente como mínimo 1800 g de hidratos de carbono y 2400 g de proteínas. Si 1 kg de maíz cuesta 0.50 euros y 1 kg de pienso cuesta 0.25 euros, calcule cuántos kilogramos de cada producto tendría que comprar el ganadero para alimentar cada día a una oveja con un gasto mínimo".

b) Represente el recinto limitado por las siguientes restricciones, calculando sus vértices
$x \geq 0 \qquad x \leq 2y+2 \qquad x+y \leq 5$

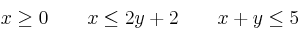
Calcule el máximo de 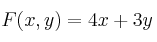$F(x,y)=4x+3y$ en ese recinto, así como el punto donde se alcanza
.
(#4376) - Selectividad Andalucía 2017 Septiembre B1

a) Represente el recinto definido por las siguientes inecuaciones:
$x+y \leq 3 \qquad 2x+y \geq 4 \qquad y \geq -1$
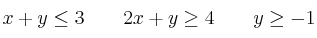
b) Razone si el punto (2, 1) pertenece al recinto anterior.
c) Obtenga los vértices del recinto y los valores mínimo y máximo de la función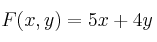 $F(x,y)=5x+4y$ en ese recinto, indicando en qué puntos se alcanzan.
d) Razone si la función F puede alcanzar el valor 9 en el recinto anterior.

Ejercicios Resueltos de Programación Lineal

Selectividad Andalucía

Matemáticas II

Mat. C. Sociales II